
by Günther Rosenbaum
Yspahan, a game by Sebastian Pauchon, was released by Ystari in October 2006.
We already published a review ) of this game. This article is about the interesting and definitely original dicing mechanism and the probabilities of different dice roll results.
 |
| It is obvious that dice on the "vase" line will not be seen very often! |
Normally, you roll 9 dice. However, you are free to add up to 3 more dice by paying for them.
The cast dice are sorted: All 1s constitute one group, all 2s, …, all 6s. These groups are placed on the board which is shown at the right hand side following these rules:
On the right hand side, you can see an example result. You'll notice that below the "gold" row, there can be gaps.
So, it's time to ask some interesting questions:
and
When optimising your strategy, it won't hurt if you have some idea about those results, and this is why I have created the tables which now follow. However, it should be clear that there are several other factors in Yspahan which determine who wins. Besides, I did not take into account the rule which allows you to add another die to an existing dice group in exchange for a special card.
| 9 W6 | min 1 | min 2 |
| Gold | 100 | 59 |
This is the table for rolling 9 six-sided dice (9 W6). All quoted numbers are rounded percentages of probabilities.
Since the group with the highest number is always placed on "gold", the probability for having at least one die there is 100%. (The latter statement is technically not true. In case all dice show the same number, they are put on the camel row. However, this is so improbable an event that the rounded probability for "gold" stays 100% in all considered cases.)
The event of "at least 2 dice (i.e. 2, 3, 4 … or 9 dice) on the the ‚gold' row" has a probability of 59%.
Attention:
If you notice a value of 100% in those tables, it is (the camels excepted) a rounded value being in
reality a number between 99,5% and 100%. Of course, for real gaming strategies, such details are
irrelevant, and that's why I kept to rounded values.
 |
| table 1
Probabilities when using 9 dice! |
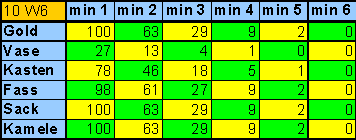 |
| table 2
Probabilities when using 10 dice! |
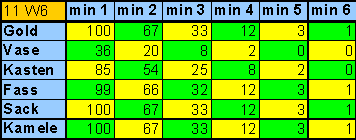 |
| table 3
Probabilities when using 11 dice! |
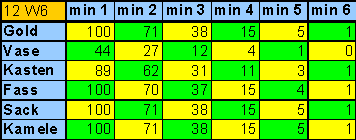 |
| table 4
Probabilities when using 12 dice |
At the start of the game, or when employing the "caravan strategy", you will probably go for "mass". You won't be picky about which spot to chose, as long as there are really lots of dice on offer!
Therefore, I've put together another table:
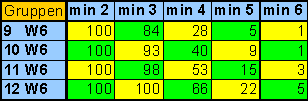 |
| table 5
Probabilities for dicing groups of a certain size! |
Everyone is free to draw his own conclusions from the tables above, and to adjust his game play accordingly. However, there are some remarks I have to make:
If the number of dice is constant, the probabilities of the lines for gold, camel, sack and barrel are, more or less, the same! As a rule of thumb, expect a group of at least 1, 2 or 3 dice with a probability of 1, 2/3 and 1/3.
This leaves the lines of chest and vase as, stochastically, somewhat more interesting.
Here is another table. It shows how the probabilities are changing when you decide to pay for adding dice to your default of 9 dice.
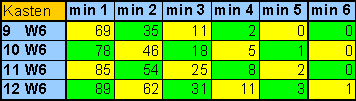 |
| table 6
Probabilities of groups of dice on the chest line, depending on the number of dice used. |
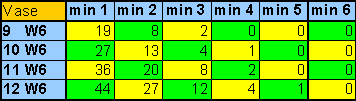 |
| table 7
Probabilities of groups of dice on the chest line, depending on the number of vase used. |
You will notice at first glance that paying for additional dice really does change those probabilities!
The victory point value on the game board is more or less like this:
2 cubes in the chest line yield 4 victory points - just as 1 cube in the vase line. Now, the probability for having at least 2 dice in the chest line is invariably higher than having at least one dice in the vase line. Hence, in the long-term average, cubes in chest line might seem somewhat more advantageous than cubes in the vase line. However, don't forget that I didn't take into account some rules (see above).
I wish all of you as much fun with this wonderful game as we've had when playing it!
| read/write comments |
©2006, Westpark Gamers