Autor Michael Tummelhofer Verlag Hans im Glück Verlag erschienen 2008 Anzahl Spieler 2-4 Spielzeit 75 Minuten Wertung

Stone Age: Die Bilanz des Steinzeitalters

analysiert von Walter Sorger

Dass wir hier als Höhlenmenschen in das Steinzeitalter versetzt werden und mittels Ackerbau, Steineklopfen und Hüttenbau die nächste Stufe zivilisatorischen Fortschritts erreichen sollen, steht in der Einleitung. Im Spiel selber fühlt man sich eher als Betriebsingenieur an den Schalthebeln eines Zufallsgenerators.

1. Grundzüge des Spielablaufs

Das Spiel verläuft in mehreren Runden. In jeder Runde verfügt ein Spieler über fünf (später mehr) Pöppel, die Zug um Zug auf den Aktionsfeldern des Spielbretts eingesetzt werden, um dadurch Besitztum zu erwerben, das nach und nach in Siegpunkte verwandelt wird. Es gibt vier Arten von Aktionsfeldern:

1. Auf Materialfeldern erhält man Rohstoffe: Nahrung, Holz, Ziegel, Steine und Gold. Ein Stück Nahrung muss man pro Runde für jeden seiner Pöppel hergeben, die anderen Rohstoffe sind die Grundlage für das Erwerben von Siegpunkten.
   
   
2. Auf Feldern mit Gebäudekarten tauscht man seine Rohstoffe in direkte Siegpunkte um.
   
   
3. Auf Feldern mit Zivilisationskarten erwirbt man gegen Rohstoffe allerlei verschiedene Vorteile, die früher oder später in Siegpunkte umgesetzt werden können.
   
   
4. Auf Potenzfeldern vergrößert man seinen Handlungsspielraum für nachfolgende Aktionen. Es gibt drei Arten davon:
   
   
   1. Beim "Werkzeugmacher" bekommt man ein "Werkzeug", das beim späteren Würfeln einem zusätzlichen Würfelauge entspricht.
      
      
   2. Auf dem "Acker" erwirbt man das Recht, pro Runde eine zusätzliche Nahrung einzustreichen.
      
      
   3. In der "Hütte" bekommt einen zusätzlichen Pöppel zum Plazieren auf den Aktionsfeldern.

Insgesamt gibt es zehn verschiedene Aktionsfelder. Auf jedem Feld darf eine festgelegte maximale Anzahl von Pöppeln platziert werden, auf den Materialfeldern sind das sieben Pöppel, auf den anderen Feldern ist es genau einer. Wer hier als erster hinsetzt, hat die entsprechend Aktion für sich gebucht, und alle Mitspieler zumindest für eine Runde davon ausgesperrt.

Auf den Materialfeldern darf man pro Spielzug so viele Plätze auf einmal belegen, wie man Pöppel hat. Wer alle seine Pöppel platziert hat, wird für den Rest der Setzrunde übergangen; er muss solange warten, bis auch die Mitspieler ihre Pöppel alle gesetzt haben.

Der Ertrag, den ein Pöppel auf einem Materialfeld einbringt, wird ausgewürfelt. Pro Pöppel gibt es einen Würfel. Die erzielten Würfelaugen werden zusammengezählt und durch die Kosten einer Materialeinheit geteilt. Eine Nahrung kostet 2 Würfelaugen, ein Holz 3, ein Ziegel 4, ein Stein 5 und ein Gold 6. Überzählige Würfelaugen verfallen. Wer z.B. 3 Pöppel auf Ziegel gesetzt hat und dort mit 3 Würfeln insgesamt 11 Augen geworfen hat, bekommt genau 2 Ziegel á 4 Würfelaugen, die restlichen 3 Augen gehen verloren. Hätte er als Pechvogel 3-mal die Eins gewürfelt, wäre er ganz leer ausgegangen.

In der Schlusswertung werden zu den Siegpunkten, die man über Gebäudekarten erworben hat, weitere Siegpunkte ausgeschüttet, die sich aus den unterschiedlichen Kriterien auf den erworbenen Zivilisationskarten ergeben. Allein durch konsequentes Sammeln von Zivilisationskarten mit "Künsten" kann man sich hier zusätzlich bis zu 64 Siegpunkte gutschreiben lassen. Wer jetzt am meisten Siegpunkte ergattert hat, ist - Sieger.

Dieser Schnelldurchgang durch die Regeln enthält manche Vereinfachung. Wer die Details genauer kennenlernen will, kauft sich am besten gleich das ganze Spiel und liest die acht Seiten Anleitungsbuch sorgfältig durch. Der Schwerpunkt meines Beitrages ist die Würfelmathematik, die bei einem erfolgreichen Spiel in "Stone Age" unbedingt berücksichtigt werden muss.

2. Würfelmathematik

Würfelt man mit einem normalen Hexa-Würfel, kann man die Augenzahlen 1 bis 6 würfeln, alle mit der gleichen Wahrscheinlichkeit. Im Durchschnitt wirft man die Augenzahl 3,5. Auf Dauer gesehen kommen alle Zahlen gleich oft vor. Das ist aber schon anders, wenn man mit zwei Würfel würfelt. Die möglichen Augenzahlen reichen von 2 bis 12, dabei kommt bei 36 Würfen die Augenzahl 1 und die 12 nur je einmal vor, die Augenzahl 7 dagegen sechsmal. Bei noch mehr Würfeln nähert sich die Verteilung der Augenzahlen immer mehr einer schönen symmetrischen Glockenkurve. (Heißt die etwa "Gauß"?) Dies ist eine triviale Zockerweisheit. Doch weil das Ergebnis ästhetisch einfach befriedigend ist (und MS-Excel das Zeichnen von alleine übernimmt), möchte ich hier die Verteilungskurven für die Ergebnisse beim Würfeln mit ein bis vier Würfeln wiedergeben.

3. Erwerb von Rohstoffen

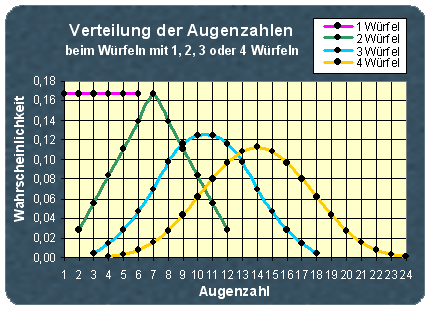
Schickt man jeweils 1 Pöppel auf die Jagd, um Nahrung zu besorgen, so erhält man für die gewürfelten Augenzahlen 1 bis 6 folgende Anzahl von Nahrungsanteilen: 0+1+1+2+2+3 = 9. Jeder Pöppel hat dann durchschnittlich 1,5 Nahrung eingebracht. Da eine Nahrung 2 Punkte wert ist, erwürfelt ein einzelner Pöppel bei der Nahrung durchschnittlich 3 Punkte.

Schickt man jeweils 1 Pöppel in die Goldmine und würfelt wieder durchschnittlich je einmal die Zahlen von 1 bis 6, so bekommt man nur jedes sechste Mal ein einziges Goldstück, nämlich für die gewürfelte 6. Alle Würfe mit den Augenzahlen 1 bis 5 bleiben ohne Ertrag. Somit erbringt jeder einzeln gesetzte Pöppel in der Goldmine durchschnittlich nur 1/6 Goldstücke. In Punkten ausgedrückt ist das nur ein einziger Punkt. Fazit: Ein einzelner Pöppel ist bei der Nahrung dreimal so viel wert wie bei Gold!

Schickt man jedoch jeweils 2 Pöppel an die Arbeit, so ändert sich dieses Verhältnis. In der Goldmine sieht die Bilanz wie folgt aus. Bei 36 Würfen erzielt man durchschnittlich 25-mal eine Würfelsumme zwischen 6 und 11 und erhält ein Goldstück. Einmal schafft man sogar eine 12 und bekommt zwei Goldstücke. Insgesamt bringen die 2 Pöppel bei 36 Versuchen 27 Goldstücke mit nach Hause. Jeder einzelne Pöppel hat also eine Erfolgsquote von 0,375 Goldstücken und das sind immerhin schon 2,25 Punkte.

Analoge Betrachtungen kann man für Nahrung, Holz, Ziegel und Stein anstellen, ebensolche für 3 oder mehr Pöppel. Insgesamt ergibt sich daraus folgende Tabelle:

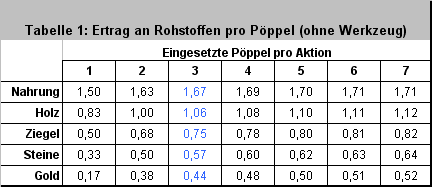
Setzt man in diese Tabelle anstelle der Rohstoffe ihren Punktwert ein (Nahrung = 2 Punkte, …, Gold = 6 Punkte), so erhält man folgende Tabelle, die den Punktwert angibt, den 1 bis 7 Pöppel mit nach Hause bringen, wenn sie gemeinsam an einer Rohstoffquellen eingesetzt wurden:

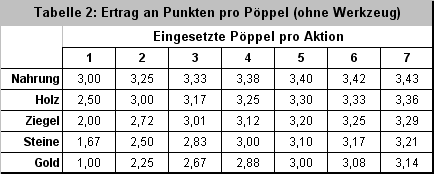
Diese Tabelle in eine Grafik gegossen ergibt folgendes Bild. Wie ein Würfelzocker erwartet, nähern sich alle Kurven dem Wert 3,5, was dem Durchschnitt der Augenzahl eines normalen Hexa-Würfels entspricht.

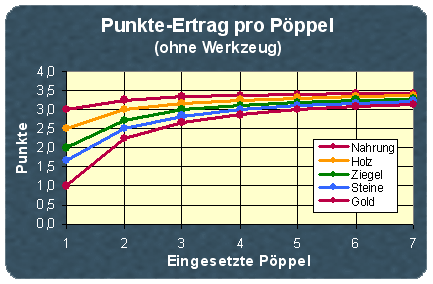
Die durchschnittlichen Erträge der einzelnen Pöppel erfahren eine weitere Veränderung, wenn man seine Leute mit Werkzeugen ausrüstet, d.h. wenn man zu allen ihren Würfen von vorneherein eine konstante Augenzahl hinzuzählen darf. Für jede Anzahl von Werkzeugen ergibt sich eine eigene Tabelle. Nur zur Demonstration dieses Effektes wollen wir uns auf die Anzahl von 3 Werkzeugen pro Wurf beschränkten.

Als Zahlenwerte erhalten wir jetzt folgende Tabelle:

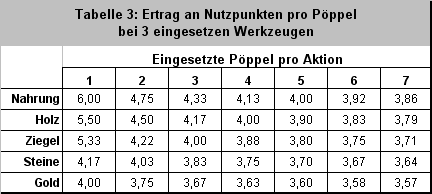
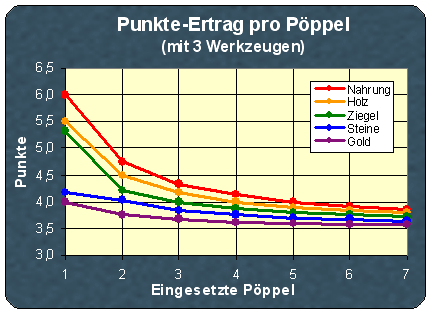
Als Grafik ergibt sich dabei folgendes Bild. Auf den ersten Blick ist hier überraschend, dass die Kurven fallen. Das liegt daran, dass sich die eingesetzten Pöppel die verfügbaren Werkzeuge teilen müssen und somit jeder nur eine entsprechenden Bruchteil ihrer Wirkung mitbekommt. Insgesamt aber verlaufen hier alle Ertragslinien deutlich höher als für die Pöppel ohne Werkzeug.

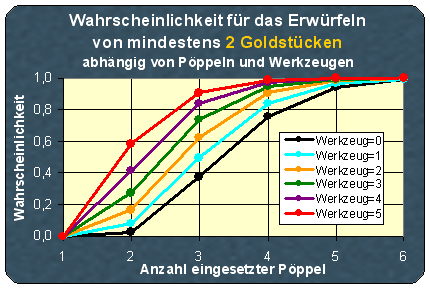
Ausgehend von der bekannten Verteilung der Augenzahlen beim Würfeln könnte man jetzt eine unbegrenzte Anzahl von Tabellen und Kurven zu den verschiedensten statistischen Fragestellungen herstellen. Z.B. wie viele Pöppel P muss man mindestens einsetzen um bei einer gegebenen Anzahl W von Werkzeugen mit einer gewünschten Sicherheit S eine Mindestanzahl eines bestimmten Materials (Holz, Ziegeln, Steinen oder Gold) zu erwürfeln. Nur exemplarisch will ich hier eine dieser möglichen Kurven angeben. Sie zeigt die Wahrscheinlichkeit für das Erwürfeln von mindestens 2 Goldstücken, abhängig von der Anzahl der eingesetzten Pöppel und der verfügbaren Werkzeuge:

4. Felderpotenz und Potenzfelder

In den folgenden Betrachtungen wollen wir versuchen, alle möglichen Zugoptionen von "Stone Age" einer Bewertung zu unterziehen und sie in eine optimale Reihenfolge zu bringen. Dazu brauchen wir zunächst eine gemeinsame Einheit, auf die wir alle Besitztümer und Vergünstigungen umrechnen. Als Einheit habe ich "Pöppel" gewählt.

Beim Umrechnen von Rohstoffen in Pöppel gehe ich davon aus, dass jeweils 3 Pöppel ohne Werkzeug eingesetzt werden, um das entsprechenden Material zu erwerben. Diese Zahl ist zwar etwas willkürlich und sicherlich kritikbedürftig, doch hier haben sich die Ertragskurven schon recht eng an ihre Asymptote angenähert und oft genug muss ein Spieler einen Teil seiner Pöppel auf anderen Aktionsfeldern einsetzen, so dass zum Erwürfeln von Rohstoffen nicht viel mehr Pöppel übrig bleiben. Außerdem haben auch die Mitspieler die begehrtesten Felder für Rohstoffe besetzt und ihren Konkurrenten nicht viele freie Felder übrig gelassen.

Die Umkehrung der blauen Zahlenkolonne in Tabelle 1 liefert den Wert in Pöppeln, die ein jeder Rohstoff kostet. Mit diesen Zahlen können wir anschließend auch noch den Wert der Potenzfelder bestimmen, die sich ja ausschließlich in Vorteilen bei der Pöppelanzahl, bei der Ernährung oder beim Würfeln ausdrücken lassen.

Diese Tabelle liefert ein wichtiges Entscheidungskriterium für den besten ersten Zug jedes Startspielers. Es stehen die Potenzfelder Acker, Hütte und Werkzeugmacher zur Auswahl. Instinktiv ahnen wir, dass es gut sein muss, sich zuallererst hier zu betätigen, denn der Gewinn ist kumulativ, er wirkt sich nicht nur einmal, sondern in jeder Runde aus.

Solange noch genügend Runden bis zum Spielende verbleiben, sind diese Felder besser als jedes andere Aktionsfeld. Und eindeutig heißt hier die Prioritätenreihenfolge: Acker (= Ernährung) geht vor Hütte (= Vermehrung) und vor Werkzeugmacher (= Würfelplus).

5. Gebäude

Gebäude werden direkt in Siegpunkte umgesetzt, indem man die dafür bestimmte Anzahl von Rohstoffen hergibt. Bei "festen" Gebäude ist Zusammensetzung der abzuliefernden Rohstoffe genau vorgeschrieben ist, bei "variablen" Gebäuden ist nur die Anzahl der Rohstoffe und die Anzahl verschiedener Rohstoffe, z.B. also "4 Rohstoffe von einer Sorte", oder "4 Rohstoffe von genau 3 Sorten".

Je höherwertig die Rohstoffe sind, die man abgeben muss, desto mehr Siegpunkte erhält man dafür. In der folgenden Tabelle sind alle Gebäudekarten mit den zugehörigen Siegpunkten aufgelistet.

In der dritten Spalte "Kosten (in Pöppel)" ist angegeben, wie viele Pöppel durchschnittlich nötig waren, die entsprechenden Rohstoffe zu erwerben. Der Zahlenwert wurde über die Summierung der Rohstoffe entsprechend den obigen eingeführten Tabellen gebildet. In der vierten Spalte wurden die erworbenen Siegpunkte durch die Anzahl der benötigten Pöppel dividiert. Diese Zahl ist ein Maß für die Effizienz eines eingesetzten Pöppel.

Aus der letzten Spalte mit den Siegpunkten pro Pöppel können wir folgende Schlussfolgerungen ziehen:

1. Die Gebäudekarten mit vielen Rohstoffen sind nützlicher als Gebäude mit wenigen Rohstoffen, sie bringen die meisten Siegpunkte pro Pöppel ein.
   Das war erwartet worden, weil hier der zusätzliche Pöppel zum Erwerben des Gebäudes am wenigsten durchschlägt.
   
   
2. Kann man auf einem variablen Gebäude beliebige Rohstoffe eintauschen, so bringt Holz die meisten Siegpunkte pro Pöppel ein, gefolgt von Ziegel, dann von Stein und erst am Ende folgt Gold.
   Das ist vielleicht überraschend, weil Holz ja absolut die wenigsten Siegpunkte ergibt. Allerdings ist das Erwürfeln von billigem Rohmaterial ja auch deutlich effizienter als das von verlustreichem Gold oder Stein. Zumindest gilt das für den Ansatz, den ich gewählt habe, nämlich die Rohstoffe ohne Werkzeuge zu gewinnen. Wer hier z.B. mit einer konsequenten Werkstoffpolitik seine Effizienz für das Erwerben höchstwertiger Rohstoffe entscheidend verbessert, kann die Rangfolge sicherlich wieder umkehren.
   
   
3. Die Gebäude mit einer fest vorgeschriebenen Anzahl von Rohstoffen sind die schlechtesten in Bezug auf Siegpunkte pro Pöppel.
   Das war auch zu erwarten, weil diese Gebäude die wenigsten Rohstoffe umsetzen und sich hier der Pöppel zum Erwerben des Gebäudes am stärksten bemerkbar macht. Das hätte aber nicht so sein müssen, denn der Spieldesigner konnte bei diesen Gebäuden die Anzahl der Siegpunkte frei vergeben, und er hätte hier durchaus ganz unterschiedliche Maßstäbe zur Geltung bringen können.

6. Zivilisationskarten

Den Durchschnittswert der Siegpunkte aus obiger Tabelle verwenden wir, um den Siegpunktwert pro Pöppel zu ermitteln. Demnach gilt die Gleichung für den "Pöppel-Faktor":

Damit können wir jetzt zu jedem beliebigen Spielelement seinen Wert in Siegpunkten berechnen. Dabei ist allerdings nicht so sehr das einzelne Element von Interesse, sondern die Menge der Zivilisationskarten, aus denen wir uns bei unseren Spielzügen ja das jeweils beste auswählen müssen.

Die Zivilisationskarten bringen Vorteile verschiedenster Art. Um eine Prioritätenreihenfolge aufstellen zu können, bringen wir alle diese Vorteile in die neu bestimmte und einleuchtende Einheit "Siegpunkte". Beim Wert der verschiedenen Rohstoffe multiplizieren wir ihren oben eingeführten Gegenwert in Pöppeln mit dem Pöppel-Faktor und erhalten damit ihren jeweiligen Wert in Siegpunkten.

Bei den Zivilisationskarten, die Siegpunkte für verschiedene Spielelemente vergeben, ist der wirkliche Wert noch abhängig von der Anzahl der Elemente, die ein Spieler bis zum Spielende aufgesammelt hat. Hier gehe ich von folgendem Endstand aus.

Diese Annahmen beruhen auf meiner bisherigen Erfahrung mit dem Spiel und sind natürlich wieder diskussionsbedürftig. Doch in der Größenordnung werden diese Zahlen wohl stimmen. Wer bessere Zahlen kennt, kann sich selber leicht eine korrigierte Tabelle zusammenstellen.

Setzt man jetzt bei allen Begünstigungen durch eine Zivilisationskarte den Zahlenwert in Siegpunkten ein, so ergibt sich folgende Rangfolge (absteigend):

Fazit: Es gibt extreme Unterschiede innerhalb der Wertigkeit von Zivilisationskarten, die wertvollste Karte bringt dreimal so viele Siegpunkte ein wie die billigste. Läppisch sind die Karten mit Einmal-Einkünften an Material oder festen Siegpunkten. Kunst ist meist lohnenswert, zumindest solange die Konkurrenz schläft und einem den Erwerb von vielen verschiedenen Kunstwerken zulässt. Am einträglichsten sind die Zivilisationskarten, die auf den Endbesitz an Pöppeln bzw. Gebäuden ein Mehrfaches an Siegpunkten ausschütten. Hier muss man zugreifen, wann immer man die Möglichkeit dazu hat, auch wenn man mal vier Rohstoffe dafür hergeben muss.

7. Spieltipps

Ergänzend zu den Tipps in der Spielanleitung lassen sich aus diesem Zahlenmaterial folgende weitere Tipps für ein erfolgreiches Bestehen im "Stone Age" ableiten:

1. Die optimale Reihenfolge beim Besetzen der "Potenzfelder" in der Mitte des Spielbrettes sind:
   Acker geht vor Hütte geht vor Werkzeugmachen.
   Bis auf wenige Runden vor Schluss ist ein Engagement auf den Potenzfeldern im jeden Fall zu empfehlen.
   
   
2. Holz hält das Steinzeitalter in Bewegung. Man kann es bei jeder Gelegenheit lukrativ einsetzen, insbesondere bei der Auswahl hochwertiger, aber teurer Zivilisationskarten. Deswegen sollte man immer einen genügend großen Vorrat von Holz besitzen. Zehn oder gar mehr Holzstücke kann man schneller loswerden, als es einem lieb ist.
   
   
3. Ziegel und Holz sind beim Eintausch gegen Gebäudekarten die effizientesten Rohstoffe. Wenn man seine überschüssigen Pöppel konsequent in Masse auf diese Erwerbsquellen schickt, sollte man sein Siegpunktkonto am dicksten auffüllen können.
   
   
4. Muss man nicht einen bestimmten Rohstoffen erwerben, sondern will man seine Pöppel mit höchster Effizienz auf irgendwelche Rohstoffe ausschicken, dann setzt am besten alle verfügbaren Pöppel auf eine einzige Rohstoffquelle. So ist der Verlust von nicht-nutzbaren Würfelaugen am geringsten.
   
   
5. Werkzeuge sind rein rechnerisch bei allen Rohstoffen im Durchschnitt gleichviel wert. Ihr größter Nutzfaktor ergibt sich da, wo man mit minimalem (Pöppel-)Aufwand mit sicherer Wahrscheinlichkeit mindestens eine Rohstoffeinheit gewinnen möchte.
   Doch grundsätzlich sollte man die Situation vermeiden, dass man von einem bestimmten Rohstoff genau eine Einheit benötigt. Um hier genügend Erwerbs-Sicherheit zu bekommen, muss man zu viele Pöppel binden.
   
   
6. Sobald man mindestens ein Werkzeug besitzt, sollte man immer auch einen "Abstauber-Pöppel" pro Runde auf die Jagd schicken. Hier bei der Nahrungsaufnahme kann man alle übrig gebliebenen Werkzeuge am effektivsten ausnützen.
   Hat man durch irgendwelche zufälligen Spielabläufe überreichlich Nahrung im Vorrat, dann sollte man den Abstauber-Pöppel in den Wald zum Holzfällen schicken. Das liefert die zweit-effektivsten Erträge.
   
   
7. Hat man viele Werkzeuge, dann darf man ruhig auch ein einzelnes Pöppel zu den höchstwertigen Rohstoffen wie Steine und Gold schicken. Gegebenenfalls muss man halt alle Werkzeuge verbraten, um wenigstens eine Rohstoffeinheit zu gewinnen. Es ist im Prinzip egal, womit man seine geworfene Augenzahl maximal ausgenutzt.
   Allerdings sollte man dabei auch den Abstauber-Pöppel nicht vergessen. Bleiben dann z.B. durch das zufällige Würfelergebnis beim Gold gleich ganze fünf Werkzeuge nicht nutzbar, so können diese dann wenigstens bei Nahrung und Holz noch weitgehend ausgenutzt werden.

Bei diesen Tipps habe ich ein"Normal"-Vorgehen vorausgesetzt, d.h. ein fürsorgliches Bemühen, seine Pöppel wohlgenährt über die Runden zu bringen. Alternativ dazu gibt es auch noch eine "Hungerstrategie": Man verzichtet grundsätzlich darauf, Nahrung zu erwerben; man lässt seine Pöppel in jeder Runde hungern und kassiert dafür jeweils zehn Minuspunkte. Stattdessen setzt man seine gesamte Pöppel-Power bei den Rohstoffen ein und macht mit der hier reichlich fließenden Siegpunktkohle den Hunger-Verlust mehr als wett. Hier heißt es möglichst schnell Pöppel vermehren, damit sich das Hungern auch richtig lohnt.

Diese Strategie schafft ganz eine andere Wertigkeit unter den verschiedenen Spielelementen, insbesondere verliert das Potenzfeld "Acker" total seine Bedeutung und die "Hütte" wird zum absoluten Favoriten. Doch auf eine weitere Analyse dieser Vorgehensweise habe ich hier verzichte.

8. Schlusswertung

"Stone Age" ist ein einfaches Spiel. Es gibt nur eine ganze Menge ganz einfacher Dinge zu tun. Es gibt wenige, klare Regeln, die Aktionen der Spieler sind in ihrer Wirkung überschaubar, auch wenn darin zuweilen ein kumulativer Effekt verborgen ist. Der Würfel gibt dem ganzen einen spielerischen Anstrich. Berechnung und Würfel halten sich sehr gut die Waage.

Mit der hier erbrachten Analyse habe ich eigentlich den spielerischen Charakter von "Stone Age" unterminiert. Es wäre schade, wenn sich jetzt jeder Spieler nur noch mit diesem Tabellenwerk an den Spieltisch setzt. Doch ich musste diese Analyse erstellen, weil es für meinesgleichen unbefriedigend ist, ein mathematisch-statistisches Spiel nur aus dem Bauch heraus anzugehen. Vielleicht darf man es dem Spiel anlasten, dass hier überhaupt solche buchhalterischen Tabellen erstellt werden können. Es gibt zu wenig wirksame, unberechenbare Interaktion der Mitspieler, die einen vorgefassten Spielplan durchkreuzen.

Doch das Spiel funktioniert, es zeigt in Aufbau und Reife die Handschrift eines Meisters, es ist von Anfang bis Ende recht kurzweilig, und wer sich gerne zwei Stunden lang einen Würfel-Optimierungskampf gegen kompetente Mitstreiter leisten will, ist hier gut bedient.

read/write comments

©2008, Westpark Gamers