Der Ritterschlag von Zavandor

Spielanalyse des Spieles "Das Zepter von Zavandor"

Autor: Walter Sorger

1. Im Walde

Wenn "Das Zepter von Zavandor" zum ersten Mal auf den Tisch liegt, wenn die Spielregeln erklärt sind und es los geht, dann fühlt man sich, als steht man im Wald. Nachts ausgesetzt, Taschenlampe und Buschmesser in der Tasche und mit dem Auftrag versehen, bis zum Morgengrauen den Waldrand zu erreichen und unterwegs dabei möglichst viele Schätze einzusammeln. In welche Richtung man gehen soll, ist nicht bekannt, wo die wertvollsten Schätze liegen auch nicht. Nur eines ist sicher, der Waldrand liegt in jeder Richtung und wenn die Sonne aufgeht, wird jeder mit seiner Ausbeute auf die Waage gestellt.

Das Spiel ist eine Weiterführung von "Outpost", mit sehr viel mehr Spielraum für die einzelnen Aktionen, mit vielen weit reichenden Abhängigkeiten untereinander und natürlich mit viel Undurchsichtigkeit, wie eine Spieleraktion auf die andere sich auswirkt.

Ob die ganze Geschichte in der Besiedelung des Weltraumes spielt (wie bei "Outpost") oder beim Ent- und Verzaubern von Edelsteinen (wie hier beim "Zepter"), ist nur ein nebensächliches Wording. Es geht um wirtschaftliche Aktivitäten, um die Ausweitung und Auslastung von Kapazitäten, um Renditen und Gewinne. Auch wenn im "Zepter" mit ganz anderen Begriffen hantiert wird, kann jeder sofort erkennen, was gemeint ist, wenn ich im Folgenden ausschließlich eine Global-Player-Terminologie verwende.

Ich will hier nicht auf die Spielregeln vom "Zepter" eingehen. Eine gute Zusammenfassung findet man im Internet unter "www.zavandor.de". Wer das Spiel noch nie gespielt hat, kann im Folgenden ohnehin nur mit viel Phantasie erahnen, wohin die Reise geht. Ich möchte mit diesem Artikel den ausgewählten Kreis von Zepter-Liebhabern ansprechen, sie tiefer in die Geheimnisse dieses Spiel einführen und Trampelpfade zeigen, wie man seine Siegchancen verbessern kann.

2. Spiele und Rechne!

Meine Ergebnisse sind nach folgendem Vorgehen entstanden:

1) Praktische Spielerprobung bei den Westpark-Gamers

2) Nachbau des Spielablaufes mittels einer Excel-Tabellen-Kalkulation.

3) Herumprobieren mit den verschiedenen Rollen bis zu einigermaßen vernünftigen Ergebnissen.

4) Ermitteln einiger wichtigster statistischer Kennwerte des Spieles.

5) Aufstellen eines Rechenmodells, mit dem aus einem beliebigen Spielstand die voraussichtlichen Siegpunkte bei Spielende vorhergesagt werden kann.

6) Analyse der guten und schlechten Züge anhand des Rechenmodells.

7) Detail-Untersuchung für verschiedene Alternativ-Entscheidungen.

Die Ergebnisse sind also keine reine Modell-Betrachtung mit all ihren Unschärfen zwischen Theorie und Praxis. Zuerst wurde jede einzelne Rolle mit Hilfe einer Simulation aber unter enger Echtheits-Relevanz zu Ende gespielt und dabei mit all den winzigen Mangelerscheinungen gekämpft, die sehr of beim Zepter für eine traumhafte Spielentwicklung fehlen.

Das anhand der statistischen Kennwerte entwickelte Betriebsmodell veranlasste immer wieder neue Versuche, in der (Simulations-) Wirklichkeit neue Strategien auszuprobieren, die Vielfalt der Artefakte, Rollen und Wissensgebiete in den Griff zu bekommen und einen in Zeit und Menge optimalen Einsatz herauszuschälen.

Das Resultat ist hier präsentiert.

3. Lebenslinien

Fangen wir mit ein paar statistischen Kennwerten zum Spiel an. Ich habe dazu natürlich nicht tausende von Spiel-Sessions absolviert und mit Papier und Bleistift die Ergebnisse festgehalten. Der Excel-Nachbau liefert das gewünschte Zahlenwerk ja quasi als Nebenprodukt mit. Und wenn Excel dann auch noch wie von Geisterhand die faszinierenden Kurven dazumalt, die einerseits die Erfahrung und Spiel-Realität widerspiegeln, und andererseits Anreize zu besserem Spiel und neuen Detail-Untersuchungen geben, dann ist das Rechnerherz und gleichermaßen auch der Spieltrieb zufrieden gestellt.

Statische, statistische Kenngrößen	Zahlenwert
Spieldauer: Das Spiel dauert (bei wenigstens einem guten Spieler) durchschnittlich:	13 Runden
Anzahl Siegpunkte: Der Sieger erzielt am Ende ca.	45-50 Siegpunkte
Umsatz: Jeder Spieler setzt ungefähr folgendes Kapital um:	470-500 Euros
Primär-Zinssatz: Ein Edelstein erbringt einen durchschnittlichen Zinssatz von:	25 %
Durchschnitts-Zinssatz: Im gesamten Spiel wird ungefähr folgender Zinssatz erreicht:	16 %
Kosten pro Siegpunkt: Ein Siegpunkt kostet durchschnittlich	14,30 Euros
Anzahl Wächter: Der Sieger besitzt am Ende	2 Wächter
Siegpunkte pro Wächter: Jeder Wächter bringt durchschnittlich:	8 Siegpunkte

Diese Kennwerte entsprechen natürlich keinem individuellen Spielverlauf, sie sind aber erste Anhaltspunkte dafür, mit welchen wirtschaftlichen Grundzahlen beim "Zepter von Zavandor" zu rechnen ist und worauf man sich einstellen muss:

· Wenn man ein neues Wissensgebiet startet, dann braucht man dazu 4 Runden, um den Siegpunkt-relevanten Level 4 zu erreichen. Ab Runde 10 klappt das in der Regel nicht mehr.

· Wenn man eine Investition tätigen will, die sich erst in den Folgerunden auszahlt, kann man überschlägig ausrechnen, ob sie sich noch lohnt. Wenn ein Edelstein beispielsweise in Runde 5 gekauft wird, dann kann er durchschnittlich noch 7 mal (13 - 5 - 1 mal) Zinsen abwerfen.

Doch wie bei jedem Wirtschaftspiel, bleiben Zinsen und Erträge nicht konstant, sie verändern sich von Runde zu Runde entsprechend den Mechanismen des Spiels.

Im folgenden Diagramm zeigen die Kurven die Entwicklung der wirtschaftlichen Kenngrößen von Runde zu Runde.

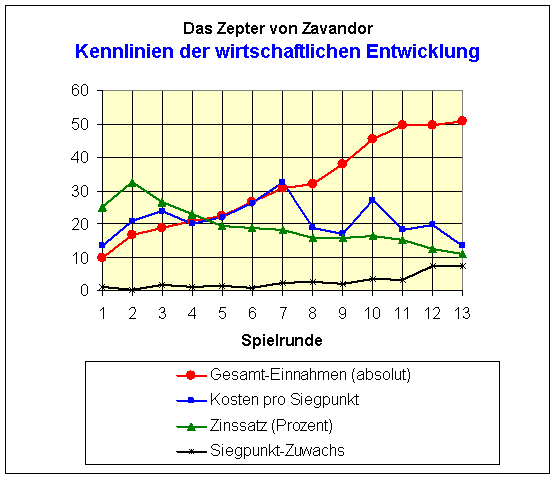
Was können wir daraus ablesen?

1) Die Siegpunkte (schwarze Linie) wachsen ganz langsam an. Bis zur 9. Runde braucht man sich keine Sorgen zu machen, wenn man pro Runde nur 1-2 Siegpunkte dazu gewinnt. Dann allerdings muss man seine Flinte geladen und in Anschlag gebracht haben. Wenn es im Endspurt darum geht, an der Ausbeute beteiligt zu sein, darf man jetzt nicht erst nach dem Pulver suchen.

2) Die Kosten pro Siegpunkt (blaue Linie) zeigt mehr Zacken, als man vielleicht vermutet. Man sollte das Auf und Ab aber nicht allzu ernst nehmen, hier fließen die unvermeidlichen sporadischen Siegpunkt armen Investitionen in die Zukunft ein. Die wesentlichste Information dieser Linie ist, dass Siegpunkte fast das ganze Spiel über weit mehr als 20 Euros kosten. Man darf hier bei seinen Investitionsentscheidungen nicht auf Siegpunkte achten, sondern auf beste Entwicklungsmöglichkeiten und Einnahmen. Erst am Ende wird die Kuh gemolken. Dann allerdings so kräftig, dass insgesamt ein Schnitt von unter 14 Euros pro Siegpunkt herausschaut. Wer jetzt nicht auf die richtigen Pferde gesetzt hat, kann nach Hause reiten.

3) Der Zinssatz (grüne Linie), berechnet aus Einnahmen für Edelsteinen und Artefakten bezogen auf den Gesamtbesitz, erreicht zu Spielbeginn Spitzenwerte von über 30 Prozent! (Hier macht sich der relativ hohe Zinssatz für 3 Opale und der Rabatt für die Hexe bemerkbar.) Ab Runde 4 fällt der relative Ertrag aber ziemlich linear von ca. 22 Punkte auf etwa 12 Punkte bei Spielende ab. Die Schlussfolgerung daraus ist: Artefakte mit einer Rendite von unter 20 Prozent sind in den ersten Runden nicht lukrativ genug. Man sollte sich zu Beginn nach etwas besserem umsehen. Erst nach Runde 5 kann man sie wieder in seine engere Investitions-Auswahl nehmen. Dann aber gleich ganz eng!

4) Die Gesamt-Einnahmen pro Runde (rote Linie) steigen selbstverständlich kontinuierlich an. Sie fangen bei allen Spielern mit ca. 10 Euro an und erreichen ab Runde 11 Werte von über 50 Euros. Neben der einfachen Beschreibung des Geldsegens, der auf jeden Spieler wartet, gibt diese Kurve aber auch klare Hinweise, ab welcher Spielrunde welche Artefakte verfügbar sind. Da man von Runde zu Runde sein Geld ja nicht sparen darf, sondern es den Spielregeln gemäß jeweils fast vollständig in den Wirtschaftskreislauf investieren muß, kann man sich Artefakte nur leisten, wenn die Einnahmen einer Runde in etwa an den Preis für die Artefakte herankommen.

4. Frühe Vögel

Die folgende Graphik zeigt die Runden an, ab der die verschiedenen Artefakte auf den Markt kommen können:

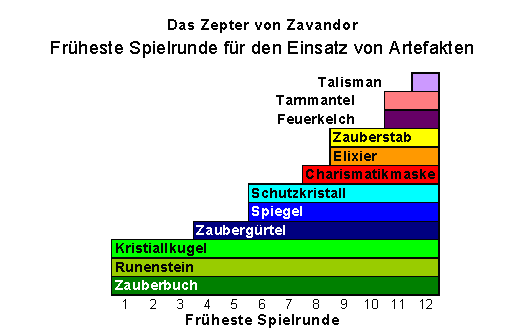
Es ist deutlich, dass außer den grün gezeichneten Billigheimern die anderen Artefakte erst zu fortgeschrittener Stunde erschwinglich sind. In der Regel erst weit in der zweiten Spielhälfte.

Wer scharfe Augen kann, kann bei der obigen Tabelle monieren, dass hier auch der "Talisman" aufgeführt ist, obwohl er mit einem Einstandspreis von 100 Euro noch weit außerhalb der Reichweite der oben beschriebenen Einnahmen von 50 Euro liegt. Und von den Wächtern mit einem Preis von 120 Euro pro Stück fehlt noch jede Spur, obwohl das Spiel angeblich schon zu Ende sein soll und folglich bis Runde 13 mindestens 5 Wächter über den Ladentisch gegangen sind. Wie das?

Hier wirkt es sich aus, dass es für die einzelnen Artefakte Ermäßigungen gibt, die den Preis drastisch senken. Ohne diese Abschläge würde das Spiel noch einige Runden länger dauern.

Damit wird auch klar aufgezeigt, dass man unbedingt etwas tun muss, um billiger an Wächter heranzukommen, als für die nominalen 120 Euro. Ansonsten wälzt man sich immer noch wie der alte Onkel Dagobert in seinen Beständen an Diamanten und Rubinen, während die drei Neffen mit den Wächtern und dem Siegeskranz schon längst über alle Berge sind.

5. Gewinn und Verlust

Langsam nähern wir uns der wichtigsten Frage im "Zepter", nämlich, in welcher Reihenfolge man welche Erwerbungen anpeilen sollte. Alle kosten Geld und alle bringen Geld. Die Kosten sind direkt am Preisschild ablesbar, die Gewinne finden sich in unterschiedlichsten Formen:

1) Einmal-Prämien in Geld

2) regelmäßig wiederkehrenden Einnahmen

3) Preisnachlässe auf spätere Erwerbungen

4) Vergünstigungen und Geschenke

5) Erweiterungsmöglichkeiten für Investitionen

Um hier Äpfel mit Birnen vergleichen zu können, muss eine Metrik gefunden werden, in der alle Effekte in Heller und Pfennig umzurechnen und dann auch noch mit den Einkaufpreisen in Relation gebracht werden können.

Die erste Frage in diesem Zusammenhang ist, welche Einbußen muss ich durch die Investition als solche hinnehmen? Jede Ausgabe für irgendein Objekt hat ja zur Folge, dass ich das Geld nicht in andere, ggf. ertragreichere Positionen investieren kann.

Da beim "Zepter" die Fülle der Investitionsmöglichkeiten und ihre Auswirkungen ein ganzes Gewirr von Wenn und Abers sind, kommen wir mit einer Detail-Betrachtung nicht weiter. Die Lösung hierfür ist eine ganz einfache Modellvorstellung:

Stellt man die durchschnittliche Besitz-Entwicklung (verifiziert aus vielen Einzelsimulationen) in einer Kurve zusammen, dann findet man, dass sie sich sehr leicht durch eine simple e-Funktion mit einem linearen Anteil darstellen lässt:

Formel 1: Intrapolation der Besitz-Entwicklung

Jetzt will ich einmal folgende Annahmen treffen: Im "Zepter" wirkt sich jede Einmal-Investition zu irgendeinem Zeitpunkt des Spieles genau proportional zur obigen Potential-Linie aus. Veranschaulicht wird diese Annahme durch das folgende Diagramm:

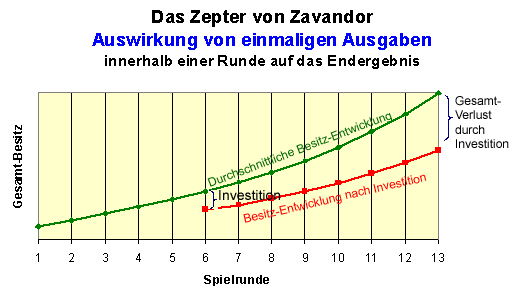
Für den Gesamt-Verlust einer Investition (ohne zunächst deren positive Effekte zu betrachten) ergibt sich demnach:

Formel 2: Extrapolation der Verlust-Auswirkung

Jeder Berufene ist hier herzlich aufgerufen, die Denk- und Rechenfehler dieses Modells aufzuzeigen. Und wenn ihm dann noch ein bisschen Esprit übrig bleibt, darf er gleich auch noch bessere Formeln auftischen.

Wir sind erst einmal zufrieden damit und nutzen die Formel 2 gleich noch einmal aus, um den Effekt einer positiven Einmal-Prämie zu berechnen. Die Schlussfolgerungen zur Besitz-Entwicklung sind ja identisch, ob ich mich durch eine einmalige Investition von der Durchschnittlinie nach unten entferne oder durch eine einmalige Siegprämie nach oben.

Es gilt also unter der Gleichsetzung Prämie = Investition:

Formel 3: Extrapolation der Auswirkung von Einmal-Prämien:

Betrachten wir jetzt noch die Effekte von anderen Arten von Einkünften:

2) regelmäßig wiederkehrenden Einnahmen (Verszinsungen):

Jede einzelne Zinseinnahme wird wie eine Einmal-Prämie betrachtet. Gemäß der Formel 3 wird ihre Auswirkung auf den Besitzstand am Ende berechnet und alle Einzelposten werden zusammengezählt.

3) Preisnachlässe auf spätere Erwerbungen

Die Preisnachlässe wirken sich ebenfalls wie Einmal-Prämien aus. Der Zeitpunkt der Prämien-Zahlung ist allerdings nicht der aktuelle Zeitpunkt im Spiel, sondern der spätere Zeitpunkt der Investition, auf die der Preisnachlass wirkt. Bei der Charismatikmaske kann z.B. davon ausgegangen werden, dass der damit verbundene Preisnachlass für Wächter erst in der letzten oder vorletzten Runde durchschlägt.

Bei der Berechnung der Nützlichkeit der Charismatikmaske ist es weiterhin von entscheidendem Einfluss, ob später ein oder zwei Wächter gekauft werden. Da der Unterschied beträchtlich ist, habe ich in den folgenden Tabellen für diese beiden Fallunterscheidungen zwei getrennte Zahlenreihen ausgewiesen.

4) Vergünstigungen und Geschenke

Bei Vergünstigungen (z.B. Erhöhung von Wissensstufen) müssen willkürliche Annahmen darüber getroffen werden, welcher Wert in diesem Vorteil liegt. Wenn ich gerade kein Wissensgebiet offen habe, dann verfällt die Vergünstigung und ich erhalte überhaupt keinen Gegenwert. Wenn ich dagegen gerade beim Energiefluss oder bei den 9 Weisen auf Stufe 3 bin, bringt mir die Erhöhung auf Stufe 4 satte 24 Euros ein.

In der folgenden Zusammenstellung bin ich von einem durchschnittlichen Gewinn von 20 Euros ausgegangen. Man muss sich schon ein bisschen anstrengen, diesen Betrag zu erzielen. Aber es muss ja das Bestreben eines jeden Spielers sein, sich diese Vergünstigungen genau in den Augenblicken zuzulegen, wenn ihre Geldvorteile sich am kräftigsten auswirken. Da ist dieser Wert-Ansatz durchaus gerechtfertigt.

Einen geschenkten Wissenstein habe ich ebenfalls mit einer Prämie von 20 Euros veranschlagt. Das ist der Preis für den ersten Wissenstein. Sehr viel mehr werden es wohl nicht werden und bei späteren Wissensteinen macht sich der Effekt von Zins und Zinseszins ohnehin nicht mehr so stark bemerkbar.

Alle diese geldwerten Vorteile wirken sich wie Einmal-Prämien aus und werden nach Formel 3 zur Berechnung ihres Effektes auf den Gesamt-Gewinn verarbeitet.

5) Erweiterungsmöglichkeiten für Investitionen

Hier bleibt noch ein Loch, das kriegen wir später.

6. Artefakte

Wenden wir jetzt unsere allgemeinen Betrachtungen zu Gewinn und Verlust jetzt auf dem Markt von Zavandor an und schauen nach, welche Musik in den Artefakten verborgen liegt.

Alles, was zu Kosten und Nutzen an Zahlen vorhanden ist und was sich nach den obigen Überlegungen darin ausdrücken lässt, ist in der folgenden Tabelle zusammengefasst.

Bei den Artefakten "Spiegel" und "Tarnmantel",

Artefakt	Kosten	Zins	Sofort Prämie	Prämie für später	für
Runenstein	20		20		Wissensstufe + 1
				10	Feuerkelch
Kristallkugel	20			5	Elixier
Spiegel	40		20		1 Wissenstein
			10		Konkurrenz verliert Edelstein
Schutzkristall	40	7,5			1 Smaragd pro Runde
Elixier	60		10		Diamant
Charismatikmaske	50		20		Wissenstufe + 1
				20	bei einem späteren Wächter
				40	bei zwei späteren Wächtern
Feuerkelch	80	15			1 Diamant pro Runde
Tarnmantel	80		20		1 Wissenstein
			10		Konkurrenz verliert Edelstein
Talisman	100				Wissenstufe + 2

Gehen wir jetzt mit diesen Zahlen in die Formeln für die Gewinn- und Verlust-Rechnung ein und lassen und uns von Excel das Ergebnis malen, ergibt sich folgendes Bild:

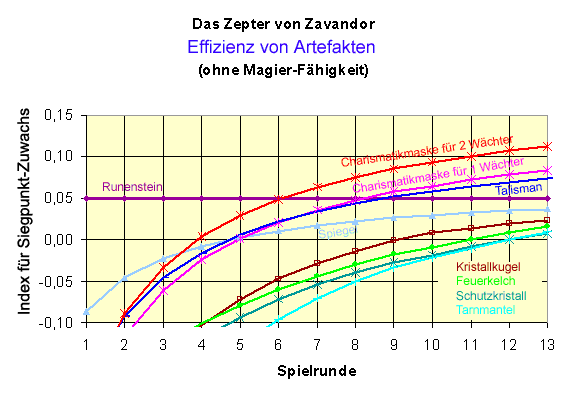
Die Kurven wurden für alle Spielrunden dargestellt, auch wenn von den Einkommensverhältnissen her ein Erwerb noch gar nicht in Frage kommt.

In dieser Kalkulation wurde vorausgesetzt, dass die Magier-Fähigkeit (Wissen um Artefakte) nicht entwickelt worden war, sondern dass zum Erwerb nur die jeweiligen Steigbügelhalter-Artefakte vorhanden waren, mit denen der Anschaffungspreis vermindert wird. Sollte ein Spieler sich auch das Wissen um Artefakte in voller Schönheit angeeignet haben, dann liegen im Prinzip alle Kurven ein paar Punkte höher, aber in der Relation untereinander hat sich nicht viel verändert.

Welche Lehren können wir aus diesen Kurven ziehen?

1) Der Runenstein (violette waagrechte Linie) ist in der Anfangsphase ein absoluter Renner. Er liegt in allen Phasen des Spieles deutlich über der Null-Linie. Warum? Man bekommt bei ihm für 20 Euro einen Siegpunkt und dazu noch eine Wissenstufe. Selbst wenn die Wissenstufe nur 16 Euro wert wäre, kostet der Siegpunkt nur 4 Euro. Eine solche Preislage können nicht einmal die Wächter in der allerletzten Runde des Spieles bieten. Geht es in der 4. Wissensstufe um 20 oder gar 24 Euros, dann ist in dieser Runde der Runenstein ein absolutes Muss.

2) Die Charismatikmasken sind in der Endphase unerreicht. Selbst wenn man hinterher nur einen einzigen Wächter ersteht, ist die Charismatikmaske ab Runde 9 von keinem anderen Artefakt zu schlagen. Bei den vom Sieger angepeilten 2 Wächtern geht ohne Charismatikmaske schon gar nichts.

Eine Voraussetzung für diese Nützlichkeit ist aber ähnlich wie beim Runenstein, dass man überhaupt irgendwo eine Wissensstufe höher steigen kann. Eine Lehre aus dieser Tatsache ist es, bis in die Schlussphase des Spieles immer wieder neue Wissensgebiete zu erschließen. Die Prämien für den Charismatiker werden es honorieren.

3) Der Theorie nach ist der Talisman in der Endphase ebenfalls ein lukratives Objekt. Hier geht ein, dass man 2 Wissensgebiete erhöhen darf. In der Praxis dürfte der Talisman aber deutlich weniger Wert haben, da er mit seinem hohen Preis ohnehin nur in der letzten Runde in Einsatz kommen kann und es einer äußerst scharfen Kalkulation braucht, hierzu genau zwei Wissensgebiete mit optimaler Stufen-Entwicklung zum Aufwerten bereit zu haben.

4) Das nächst lohnende Objekt der Begierde ist der Spiegel. Er ist auch leichter erschwinglich als die genannten Paradepferde für den Schlusskampf, und schon ab Runde 5 liegt seine Rendite über Null, d.h. dieses Artefakt bringt ab diesem Zeitpunkt mehr ein, als der Durchschnitt aller anderen Investitionsmöglichkeiten.

5) Die übrigen Artefakte liegen in ihrem Wert nicht viel auseinander. Vor allem auch dann, wenn es auf das Ende zugeht. Sofern man damit keinem Mitmenschen eine Freude machen will, wird es wohl das beste sein, dieses Objekte links liegen zu lassen.

7. Buch schlägt Gürtel

Einem aufmerksamen Leser ist vielleicht aufgefallen, dass in der obigen Darstellung drei Artefakte total ignoriert wurden: Zauberbuch, Zaubergürtel und Zauberstab. Sie sind in das bereits erwähnte Loch gefallen, das ich hier schließen will.

Die Wirkungen dieser Artefakte auf die Sieg-Bilanz ist nur sehr schwer zu ermitteln. Die Vorteile liegen hier ja nicht in relativ durchsichtigen Zahlen auf der Hand, sondern es sind Versprechungen in die planerische Zukunft: Verbesserungen in Produktionskapazitäten und Verbesserungen in Produktions-Qualität. Der Größenwert der damit erzielbaren Gewinne sind total abhängig von der sonstigen Investitionspolitik des Spielers.

Ich habe es mir erspart, die tausend möglichen Varianten einzeln zu unterscheiden. Meine Simulationen haben aber erbracht, dass für die Hexe, den Magier und den Kobold das Zauberbuch (Zulässigkeit von Smaragden) als erstes Artefakt um einige Milligramm günstiger als der Zaubergürtel (mehr Platz für Edelsteine). Der Elf fährt dagegen mit dem Zaubergürtel deutlich besser. Der Druide sollte beide wohl oder über links liegen lassen. Warum das so ist, werde ich später unter bei der Bewertung der verschiedenen Rollen noch erklären.

Bei der Fee ist für die Entscheidung zwischen Buch oder Gürtel ein Fotofinish notwendig. Die beiden Artefakte sind für sie ungefähr gleich viel wert.

Den Zauberstab habe ich in dieser Betrachtung ganz weggelassen. Er steht mit keinem anderen Artefakt in Konkurrenz. Wen der Hafer sticht, kann ihn sich zulegen. In meinen Sieger-Strategien hat er kein einziges Mal von sich reden gemacht.

8. Siegpunkte

Im Diagramm zur Nützlichkeit der Artefakte steht in der Ordinate das Kriterium "Index für Siegpunkt-Zuwachs". Dies ist die erwartete Siegpunkt-Differenz im Vergleich zum Normalverbraucher, bezogen auf den Kaufpreis für das jeweilige Artefakt.

Es kommt beim "Zepter" aber natürlich nicht nur darauf an, für wenig Geld viel zu bekommen, sondern er kommt vor allem darauf an, für viel Geld am meisten zu bekommen. Und richtig Zaster gewinnt macht man nicht mit Runensteinen, sondern mit Wächtern.

Die Kosten pro Siegpunkt sind hier natürlich extrem abhängig von den Preisnachlässen, die man für diese Objekte via Magierwissen und Charismatikmasken vorgeplant hat. Die nachfolgende Tabelle fasst die Ergebnisse zusammen. Zum Vergleich sind die Werte für die Artefakte Talisman und Tarnmantel (bei optimalen Einkaufbedingungen) ebenfalls aufgeführt. Wächtern ohne Charismatik können sie durchaus das Wasser reichen.

Artefakt		Wächter			Talisman	Tarnmantel
Siegpunkte		8			8	5
Billigmacher		Charismatikmasken				Zauberbuch
		0	1	2
Höchstes Wissen um Artefakte	Preis:	100	80	60	90	55
	Kosten pro Siegpunkt:	12,5	10,0	7,5	11,3	11,0
Kein Wissen um Artefakte	Preis:	120	100	80	100	65
	Kosten pro Siegpunkt:	15,0	12,5	10,0	12,5	13,0

Ganz unangefochten steht ein Wächter mit doppelter Charismatik hier an der Spitze. Für nur 60 Euro bekommt man ca. 8 Siegpunkte. Wer bei diesem Geschäft zweimal zuschlagen kann, wird von keinem weiteren Schatzgräber übertroffen.

9. Tanz der Edelsteine

Edelsteine sind der Motor vom "Zepter". Bei Spielbeginn dürfen nur Opale und Saphire gekauft werden. Der dritte Opal hebt ihre Durchschnittsrendite auf stolze 33 Prozent. Das wird nirgendwo anders geboten. Ganz klar muss jeder Spieler zuallererst den dritten Opal kaufen, bevor er sich nach anderen Edelmarken umschaut.

Die Saphire bringen immerhin, wie alle anderen Edelsteine auch, eine Rendite von 25 %. An die vorhandenen Kapazitätengrenzen zu gehen, schreibt schon allein die Binsenweisheit jedes Wirtschaftspiels vor: "keep fully invested". Also füllen wir alle vorhandenen Plätze so schnell wie möglich mit Saphiren auf. Und dann? Sollen wir uns mit den beiden anfänglichen Edelsteintypen bescheiden oder sie früher oder später in höherwertige Edelsteine umtauschen? Zu welchem Zeitpunkt?

Das ist selbstverständlich keine Frage von Lust und Laune. Auch hier scheidet die gleiche nüchterne Rechnerei die guten von den schlechten Aktionen.

Opale darf man praktisch niemals gegen Saphire austauschen. Selbst der allerdümmste Opal mit seinen Einkünften von 2 Euro kann seine Rolle gegen den Saphir aussitzen. Beim Tausch verliert man die Hälfte des Opalpreises und gewinnt keinen einzigen Siegpunkt dazu; als Gegenleistung erhält man lediglich um 3 Euro erhöhte Zinseinnahmen. Bei dem Differenzpreis von 15 Euro braucht man allein 5 Runden, nur um die Ausgaben neutralisiert zu haben. Soviel Zeitverschwendung wird von der Konkurrenz beim "Zepter" nicht toleriert.

Aus dem gleichen Grunde werden Saphire praktisch nie gegen Smaragde ausgetauscht. Als Austauscher lohnen sich nur die höchstwertigen Diamanten und Rubine. Smaragde und Diamanten werden gar nicht ausgetauscht. Wenn sie überhaupt gekauft werden dürfen, ist die verbleibende Spielzeit viel zu kurz, um den Tauschpreis auszugleichen.

Wir können uns in unseren Tabellen und Diagrammen also damit bescheiden, Opale und Saphire gegen den Smaragde, Diamanten und Rubine einzutauschen. Die Überlegung zu den Formeln und Rechnungen ist einfach: Auf der Haben-Seite eines Edelstein-Tausches steht der Zugewinn an Siegpunkten und die erhöhten Zinszahlungen, die nach der Zinseszins-Formel bewertet werden; auf der Soll-Seite steht der Kaufpreis, der nach der gleichen Formel wir bei der Artefakten-Diskussion zu einem Gesamt-Verlust extrapoliert wird. Für die Extrapolation bin ich von einem durchschnittlichen Zinsniveau von 16 % ausgegangen. Bei den Opalen habe ich nicht unterschieden, dass bei 1, 2 oder 3 Opale jeweils andere Zinszahlen gelten, sondern ich habe einen Durchschnittszins von 33 % angesetzt. Einzel-Opale sind mit noch größerer Berechtigung auszutauschen.

Von Excel gemalt sehen die Rentabilitätskurven für einen Edelstein-Tausch wie folgt aus:

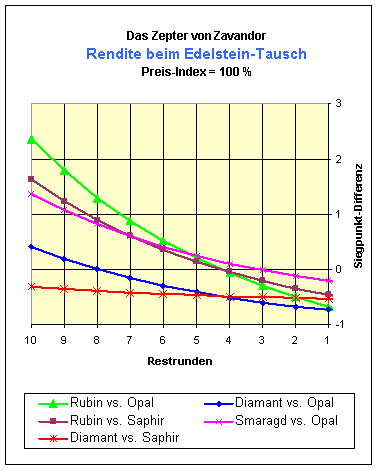
Für die Restrunden (= noch zu spielenden Spielrunden), bei denen die Rendite größer ist als 0, lohnt sich ein Tausch, für die Restrunden mit Rendite unter 0 lohnt sich der Tausch nicht mehr. Man sieht, dass bei mehr als 5 Restrunden jeder Edelstein-Tausch in Rubine noch Gewinn bringt. Ein Tausch von Opalen gegen Smaragde lohnt sich bis zu 3 Runden vor Schluss. Hier macht sich unter anderem bemerkbar, dass ein Smaragd für nur 30 Euros 2 Siegpunkte bringt. (Smaragde sind schon allein aus dem Verhältnis Kosten pro Siegpunkte die allerbeste Wahl!)

Die rote Linie, Diamanten vs. Saphire, hätte ich auch gleich weglassen können, so traurig verläuft sie total unterhalb der Null-Linie. Bei der Fülle von anderen günstigen Gegebenheiten auf dem Markt von Zavandor ist es eben keine gute Idee, mit Diamanten sein Glück zu versuchen.

Alle Tauschbetrachtungen erhalten aber eine ganz andere Gewichtung, wenn man beim Edelsteinkauf Rabatt bekommt, d.h. wenn man nur einen Bruchteil des Preises dafür zu bezahlen hat. Kann man im Extremfall einen Rubin für 60 % des Kaufpreises erstehen, so zahlt man 36 Euros dafür und bekommt dann durchschnittlich 15 Euros Zinsen pro Runde. Das ist eine Riesenrendite von fast 42 %. Unter diesen Umständen muß der gesamte Edelstein-Tausch noch einmal neu durchgerechnet werden.

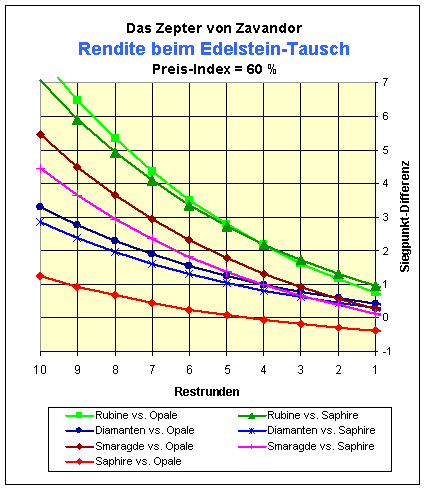
Die Linien der Rendite für die lukrativsten Tauschaktionen über die Anzahl der noch zu spielenden Runden sind im folgenden Diagramm dargestellt:

Wie nicht anders zu erwarten, lohnt sich bei hohen Rabatten ein Tausch bis in die letzte Runde.

Der Vollständigkeit halber ist in der folgenden Tabelle aufgeführt, für welche Kombination von Edelsteinen und für welchen Rabatt zwischen 0 bis 40 % bis zu viele Spielrunden vor Schluss sich ein Edelstein-Tausch unter den erwähnten Zinsannahmen noch lohnt. Bei Opalen ist dabei immer von einem 3er-Paket ausgegangen, weil nur solche Grüppchen sich überhaupt bis in höhere Runden halten können.

Bis zu wieviel Runden vor Spielende lohnt sich ein Edelstein-Tausch
Tausch-Aktion	Rabatt 0 %	Rabatt 10 %	Rabatt 20 %	Rabatt 30 %	Rabatt: 40 %
Rubin gegen Opal	5	3	1	Immer	Immer
Rubin gegen Saphir	4	2	Immer	Immer	Immer
Rubin gegen Smaragd	Nie	9	5	2	1
Diamant gegen Opal	8	5	3	2	Immer
Diamant gegen Saphir	Nie	5	2	1	Immer
Diamant gegen Smaragd	Nie	Nie	Nie	Nie	6
Smaragd gegen Opal	3	1	Immer	Immer	Immer
Smaragd gegen Saphir	Nie	Nie	Immer	Immer	Immer

Den jeweils erzielbaren Zinssatz für den Edelsteintausch kann sich der geneigte Leser selber ausrechnen. Das geht sogar während des Spieles (ggf. mit einem Taschenrechner) und wenn dabei ein Wert größer als 16 herauskommt, dann sollte der Umtausch von Vorteil sein.

10. Rollenspiele

Wenden wir uns mit unseren gesammelten Erkenntnissen jetzt den einzelnen Rollen zu und analysieren deren artgerechtes Verhalten.

10.1. Hexe (Wissen über Edelsteine)

Der Hexe bietet sich die größte Freiheit auf dem Edelstein-Markt. Sie kann und sollte jederzeit bedenkenlos ihren Besitz umschichten, d.h. ihre billigen Steine verkaufen (bei Platzmangel) und sie durch die höchst-wertigen Edelsteine ersetzen. Das Problem für sie ist nur, sich das Recht auf höherwertige Edelsteine zu erwerben.

Vom Start weg muss sie in jeder Runde ihre Wissen um Edelsteine bis zur Stufe 3 erhöhen; die 4. Stufe darf sie noch verzögern, für ihr aktuelles Einkommen ist der Preis doch sehr hoch und sie sollte sich erst darum bemühen, Platz für ihre verbilligten Investitionen zu schafften und zu füllen, bevor sie den Einkaufspreis noch weiter senkt.

Für ihre Kapaziätserweiterungen ist das Zauberbuch lukrativer als der Zaubergürtel, weil sie beim Umstieg auf Smaragde deutlich mehr Masse anlegen und sich höhere Zinseinnahmen verschaffen kann, als für zwei zusätzliche Saphire.

Auf Rubine (Wissen des Feuers) braucht die Hexe nicht zu spekulieren. Der Weg dazu ist für ihre überall günstigen Einkaufmöglichen viel zu weit.

Im folgenden Diagramm ist der erzielte Gesamt-Rabatt meiner besten Hexe im Verlauf des Spieles dargestellt.

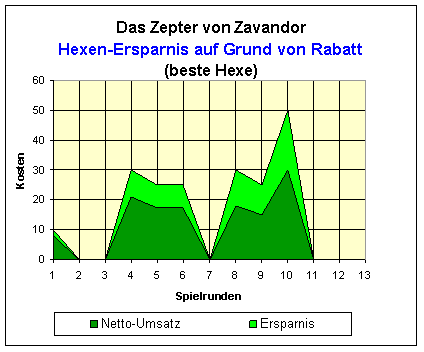
Der erste dicke Batzen zwischen den Spielrunden 3 und 7 spiegelt den Umstieg auf Smaragde wieder, der zweite dicke Batzen zwischen den Spielrunden 7 und 11 ist die Kapazitätserweiterung durch den Zaubergürtel. Diamanten oder Rubine hat sich die beste Hexe gar nicht erst zugelegt.

Bei diesem Diagramm darf man sich nicht einbilden, die hellgrüne Fläche sei ein Maß für die Gesamtersparnis. Da der jeweils ersparte Wert auf einer Zinseszins-Ebene angelegt werden kann und somit quadratische Früchte trägt, entspricht die Gesamtersparnis eher einem Rotationskörper, der entsteht, wenn man die Fläche am rechten Rand um die Y-Achse rotieren lässt.

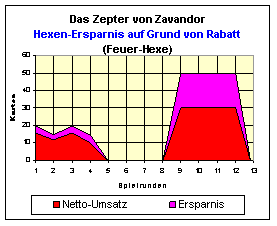
Zum Vergleich will ich noch das Rabatt-Diagramm der "Feuer-Hexe" aufzeigen. Dieser Hexentyp versucht, so früh wie möglich (aber nicht mit dem Kopf durch die Wand) an Rubine heranzukommen um die günstigen Einkaufspreise auf die teuersten Objekte anwenden zu können. So kann sie zwar bis Spielende nach absolutem Zahlen die höchsten Rabattsummen ausweisen; sie werden aber erst so spät erzielt, dass der oben erwähnte gedachte Rotationskörper vom Volumen her deutlich kleiner ist. Die Feuer-Hexe nimmt bei meinen vielen Hexen-Versuchen immer den letzten Platz ein.

10.2. Elf (Wissen des Energieflusses)

Der Elf hat ein stressfreies Leben. Er braucht seine Tage und Nächte nicht schlaflos damit zu verbringen, über Möglichkeiten zur Kapazitätserweiterung zu grübeln. Mit der naturgegebenen Zielvorgabe, sein Wissen um den Energiefluss zu erweitern, ist seine Phantasie ausreichend ausgelastet. Dieser Wissensausbau erschließt Einkommensquellen auf beträchtlichem Niveau. Die erste Wissensstufe, bringt vorzügliche 33 % Rendite, die dritte Stufe immerhin noch den guten Marktschnitt von 25 %, erst die letzte Stufe liegt deutlich darunter. Man sollte diese Stufe auch nur dann erklimmen, wenn sie einem durch das entsprechende Artefakt praktisch nachgeschmissen wird.

Wenn die Einkommensquellen des Elf kräftig genug sprudeln, legt er sich einen Zaubergürtel zu und füllt seine Kisten mit Saphiren. Ein Zauberbuch passt auch noch in seine Sammlung, bevor er sich zum Endspiel um die Wächter aufmacht. Kampflos, leidenschaftslos, und leider auch erfolglos.

Ich mag diese Rolle nicht. Sie entspricht dem angeborenen Mittelmaß. Wann immer man versucht, auszubrechen und sein Glück auf anderen, extremeren Wegen zu versuchen, zieht man den Kürzeren.

10.3. Druide (Wissen über das Feuer)

Der Druide ist ein armes Schwein. Der wesentliche Vorteil, mit dem ihn das Schicksal ausgestattet hat, ist das Recht, sich Rubine zu kaufen. Natürlich nicht sofort, sondern erst auf dem Höchststand seines Wissens um Feuer. Bis dahin ist es ein dornenreicher Weg. Man muss zusätzlich noch 45 Euros Lehrgeld hinblättern. Wenn der Druide sofort in diese Richtung loszieht, steht er nach 4 Runden quasi mit leerem Geldbeutel vor den Regalen mit den sündhaft teuren Rubinen. Jetzt muss er noch viele Runden sein Taschengeld sparen, bis er den ersten Rubin erstehen kann. Und für den zweiten dauert es fast genauso lange; inzwischen schielen die Mitspieler alle schon längst in Richtung Wächter.

Der Druide könnte fast auf den Gedanken kommen, auf diesen Rubin-Frust ganz zu verzichten und allein mit seinen 10 Euros Startvorteil einen eigenen Weg zum Glück zu suchen. Dann kann er im Endeffekt aber keinesfalls besser sein, als der Kobold, der ebenfalls mit 10 Euro mehr als die anderen auf die Reise geschickt wird, zusätzlich aber noch erhöhte Edelstein-Kapazitäten aufweist.

Um sein Geburtsrecht zu nutzen muss sich der Druide deshalb früher oder später an die Rubine heranmachen. Hier liegt ein Grund, warum für ihn Zaubergürtel und Zauberbuch gleich uninteressant sind. Er braucht weder seine Qualität zu verbessern, weil er es hier ohnehin auf das Maximum, die Rubine abgesehen hat. Und er braucht seine Quantität nicht zu erhöhen, weil er mit seinen Rubinen ohnehin nur eine kleine Kapazitätsauslastung erzielen kann. Aber erst mal muss er einen bestimmten Lebensstandard erreichen, andere Erwerbsquellen erschließen und danach streben, die Rubine etwas tiefer zu hängen.

Eine gute Idee ist es, sich vor dem Marsch auf die Rubine das Wissen um Edelsteine zuzulegen. Damit kann man die Preise für Edelsteine erheblich herabsetzen und so die Totzeit nach den getätigten Investitionen reduzieren. Diese Begabung wurde der Hexe von Haus aus in die Wiege gelegt und ihr macht es Spaß, damit zu spielen. Beim Druiden ist daraus bitterer Ernst geworden und er muss scharf kalkulieren, zu welchem Zeitpunkt er hier aktiv wird. Die Entwicklung des neuen Wissensgebietes frisst zusätzliches Geld, das dem produktiven Kreislauf entzogen wird.

Solange man noch kärglich sein Dasein fristet, kann man sich weder Feuer noch Edelsteine leisten. Wenn man aber zu spät mit dem Lernen anfängt, kann man das benötigte Wissen nicht mehr lange genug ausnutzen. Es muss einen optimalen Zeitpunkt geben, mit dem Lernen zu beginnen.

Die Frage nach dem Optimum ist noch ein bisschen kniffeliger. Die Wissenstufen dürfen ja nicht unabhängig voneinander erhöht werden, sondern in einer Runde immer nur eine von beiden. Jetzt gilt es, neben dem günstigsten Zeitpunkt auch noch die Reihenfolge zu ermitteln, in der die jeweiligen Wissensstufen erklommen werden. Die folgende Kurve zeigt die Ergebnisse.

In dem zugrunde gelegten Modell entwickelt sich der Druide zuerst nach den üblichen Gegebenheiten des Marktes. Dann fängt er ab einer bestimmten Spielrunde an, die fraglichen Wissensgebiete auszubauen. Sobald er beim Feuer die Wissenstufe 4 hat, kauft er Rubine, wann immer es ihm seine Geldbörse zulässt. Wenn er in einer Runde sparen muss, erhöht er trotzdem das Wissen um Edelsteine.

In der roten Linie erwirbt er sich zuerst das Wissen um Edelsteine bis zur Stufe 4 und fängt dann erst an, sich um die Rubine zu kümmern, in der blauen Linie erwirbt er erst zuerst das Wissen um Feuer; nach der Berechtigung auf Rubine, bemüht er sich über das Wissen um Edelsteine, ihren Preis erschwinglicher zu machen.

Das Diagramm demonstriert, dass es am sinnigsten ist, sich ab der 8. Runde beim Wissen um Feuer zu engagieren.

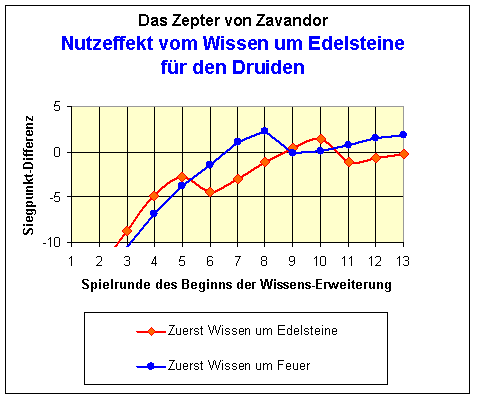
Ein kritischer Kopf kann sich jetzt noch um den Verlauf der roten Kurve Gedanken machen. Mit Recht! Was heißt es denn, wenn sie hier bei Spielrunde 10 ein Maximum hat? Was bedeutet dieser Wert? Wenn man ab der 10. Runde erst anfängt, sich um die Preise zu kümmern, dann bekommt man doch überhaupt keine Ware mehr!

Genau dieser Effekt ist hier gezeigt. Vor allen Einkäufen zuerst auf Rabatte hinzuarbeiten, lohnt sich für den Druiden überhaupt nicht. Je später er diese Fehlplanung verfolgt, desto besser, d.h. desto weniger Verluste bereitet ihm sein Fehler. Wenn er aber zu spät mit den Rabatten anfängt, dann bekommt er noch nicht einmal den Bonus von 2 Siegpunkten für die Stufe 4 in einem Wissensgebiet. Wenn er aber genau in Runde 10 mit dem Wissen um Edelsteine anfängt, dann bekommt er gerade soeben noch den Bonus, allerdings verschont ihn das Spielende vor der Dummheit, sich noch mit den Rubinen zu verzetteln. Q.e.d!

10.4. Fee (Wissen der 9 Weisen)

Die Fee schwimmt zu Spielbeginn im Geld. Bevor es losgeht bekommt sie schon zwei Anteilscheine für Opale geschenkt, dann bringen ihr einmalige Investition von 6 oder 12 Euro gleich Prämien von 15 bzw. 20 Euros ein. Im Prinzip setzt sie ihr Taschengeld ein und kommt mit einem Tagelohn zurück. Damit kann sie sich freudigen Mutes auf dem Edelsteinmarkt umsehen. Sie muss es sogar, denn Sparen ist nicht erlaubt.

Leider gibt es noch nicht so viele verlockende Angebote, dass sie ihr Geld günstig loswerden könnte. Kapazitäten und Qualitäten kann sie nicht gleichzeitig verbessern, so hoch sind die Prämien dann auch wieder nicht. Schnell hat sie ihren Geburtsvorteil ausgenutzt und verspielt, bevor er ihr richtig auf die Sprünge helfen konnte.

Dann holt sie der graue Alltag mit Zaubergürteln, Zauberbüchern und weiß der Kuckuck alles ein. Am Ende liegt sie zwar gut im Rennen, für die Siegespalme reicht es aber nicht.

10.5. Kobold (Wissen der Speicherung)

Der Kobold kann von Haus aus einen Edelstein mehr für sich arbeiten lassen als die anderen. Erhöht er sein "Wissen der Speicherung" noch mal um zwei Stufen (kostet insgesamt 12 Dollar), so bekommt er einen weiteren Speicherplatz und hat jetzt ohne teure Investitionen auf dem Artefakte-Sektor insgesamt 7 Arbeitsplätze für seine produktiven Perlen. Damit kann er auch mit billigen Edelsteinen erhebliche Absolut-Einnahmen erzielen.

Da damit das Kapazitäten-Problem für ihn gelöst ist, muss er sich nur noch um die Qualität seiner Produktion kümmern. In Lande "Zavandor" heißt dies: zuerst das Zauberbuch. Den Zaubergürtel braucht er überhaupt nicht, dafür reichen seine Privilegien als Kobold. Mit einem guten Händchen für seine weiteren Aktivitäten auf dem Wirtschaftssektor kann er einen sehr guten Platz herausfahren.

10.6. Magier (Wissen über Artefakte)

Der Magier ist der alternative Esoteriker unter allen Metaphysikern von "Zavandor". Während die anderen sich mehr oder weniger dicht um die Edelsteine drängen, kann er sich fast unbehelligt bei den Artefakten tummeln. Alles ist um erhebliche Prozentzahlen billiger und wenn er die Artefakte in geschickter Reihenfolge einsetzt, so dass sich gegenseitig unterstützen, kann er sogar auf 3 Wächter kommen, während seine Kollegen noch an den Rezepten für ihre Elixiere feilen.

Mehr dazu im übernächsten Kapitel.

11. Wissen ist Geld

Ein wichtiges Spielmerkmal fehlt noch in unseren Betrachtungen: Die Wissensgebiete. Sollen wir, oder sollen wir nicht uns außer um die angeborenen auch noch um erwerbbare Wissensgebiete kümmern. Die Antwort heißt ganz klar "Ja". Wissensgebiete bringen materielle Vergünstigungen, die auch bei umkämpften Handelsspannen nicht zu verachten sind. Dazu kommt noch, dass gewichtige Vorteile mancher Artefakte erst dann genutzt werden können, wenn überhaupt angefangene Wissensgebiete vorhanden sind.

Ich will nicht mehr detailliert auf jedes Wissensgebiet eingehen. Nur die wichtigsten Fakten im Schnelldurchgang.

Wer keinen Zauberbuch und kein Elixier ersteigert hat, kann seine Produktion nur noch über Rubine auf Vordermann bringen. Dazu braucht er das Wissen um Feuer. Auch wenn es nur ein saurer Apfel ist. (Siehe Druide.)

Das Wissen um Edelsteine ist immer erfreulich. Warum sollten wir uns nicht bemühen, unsere Investitionen günstiger zu bekommen. Dass damit aber auch viel Schweiß und Tränen vergossen werden können, ist ebenfalls beim schon Druiden angedeutet worden. Und wenn unsere Investitionen im Wesentlichen schon abgeschlossen sind, dann ist das Edelstein-Wissen Schnee von gestern. Null-Investitionen können nicht billiger werden.

Energiefluss: Eine Rendite von 22-24 % für die Erhöhung der Wissensstufe klingt nicht schlecht. Da aber erst der Wissenstein erworben werden muss und die Kosten dafür auf der Negativ-Seite zu Buch schlagen, je früher desto mehr, möchte ich für den Energiefluss meine Hände nicht ins Feuer legen.

Das Wissen um Artefakte lohnt sich, wenn man viele Artefakte kauft. Für die paar dicken Hunde am Ende lohnt sich der ganze Zinnober wohl nicht. Aber hier lasse ich mich gerne eines besseren belehren. Schließlich ist der Magier ja meine Lieblingsrolle.

Bleibt noch das Wissen um die 9 Weisen. Bei der Fee ist schon angedeutet, dass hier eine kleine, aber sichere Sofort-Rendite angezapft werden kann. Wenn wir uns unbedingt bis zum Spielende noch ein Wissensgebiet zulegen wollen, dann ist das Wissen der 9 Weisen ein ideales Betätigungsfeld. Jede Stufenerhöhung zahlt sich umgehend aus. Wir können auf jeder Stufe beliebig stehen bleiben und uns im passenden Augenblick von einer Charismatikmaske ins Ziel tragen lassen.

Es gibt für die 9 Weisen jedoch einen optimalen Einsatzpunkt, bei dem die eigene Einnahmensituation, das allgemeine Zinsniveau und die Prämien für die Erhöhung der Wissensstufen in einem ausgewogenen Verhältnis stehen. Für die Fee ist dieser Zeitpunkt naturgemäß am Anfang des Spieles. Für die anderen Spieler gilt das keineswegs. Im nachfolgenden Diagramm zeigen die grüne und die rote Linie, wann für eine Nicht-Fee mit und ohne Charismatik-Maske (zur kostenlosen Erhöhung auf Wissenstufe 4) der optimale Zeitpunkt für den Beginn der Wissensentwicklung gegeben ist. In beiden Fällen liegt er zwischen der siebten und der zehnten Runde. Vorher verliert man zuviel Kapital beim Einsatz, nachher klappt es nicht mehr, die wichtige Wissenstufe 4 zu erreichen.

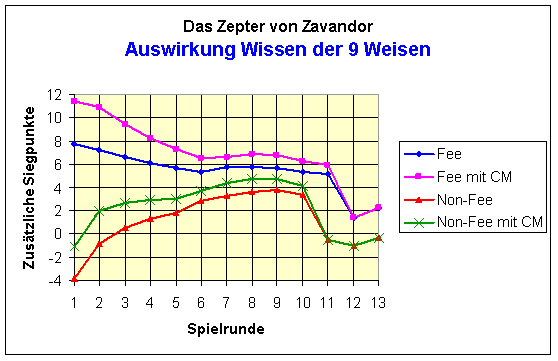
Die 9 Weisen besitzen noch einen weiteren wichtigen Vorteil, den jeder Spieler langfristig planen muss: Dadurch, dass die Prämien-Ausschüttung erst in der nächsten Runde erfolgt, kann man sich kurzfristig mal ein größeres Finanzpolster zulegen, als nach dem allgemeinen Investitionsgebot zulässig. Damit kann man gezielt eine wichtige Entwicklungsstufe erklimmen (Erwerb eines teuren Edelsteins oder eines lebensnotwendigen teuren Artefaktes), die anderenfalls erst mehrere Runden später möglich wäre. Der konkrete Einsatz hängt natürlich von der aktuellen Ausgangslage eines Spielers ab, auf den hier bei der allgemeinen Erörterung nicht eingegangen werden kann. Aber in Betracht ziehen muss es der Gewinner von Zavandor unbedingt.

12. Der Sieger

Für mich besitzt nach all meinen Untersuchungen der Magier die Favoritenrolle des ganzen Spieles. Er kümmert sich mit deutlich weniger Leidenschaft um den Edelstein-Markt. Er handelt mit Artefakten und kauft sie in der Reihenfolge, dass ihre gegenseitigen Begünstigungen sich optimal auswirken.

Seine Sieger-Aktivitäten sehen in etwa wie folgt aus:

Runde	Aktion
1.	Kauf des 3. Opals. Wissen um Artefakte auf Stufe 2
2.	Wissen um Artefakte auf Stufe 3
3.	Kauf des 2. Saphirs (Plätze für Edelsteine ausgebucht) Kauf einen Runensteins und damit Erhöhen des Wissens um Artefakte auf Stufe 4
4.	Kauf des Zaubergürtels (jetzt Platz für 7 Edelsteine)
5.	Kauf des 3. Saphirs
6.	Kauf des 4. Saphirs
7.	Kauf des Spiegels und damit Wissenstein zum Wissen der 9 Weisen. Erhöhen des Wissen der 9 Weisen auf Stufe 1
8.	Kaufen Schutzkristal. Erhöhen des Wissens der 9 Weisen auf Stufe 2
9.	Kaufen 1. Charismatikmaske und damit Erhöhen des Wissens der 9 Weisen auf Stufe 3
10.	Kaufen 2. Charismatikmaske und damit Erhöhen des Wissens der 9 Weisen auf Stufe 4
11.	Kaufen 1. Wächter
12.	Kaufen 2. Wächter
13.	Kaufen 3. Wächter (für die Kaufsumme Verkauf eines Saphirs) Ende des Spiels mit insgesamt 47 Siegpunkten.

13. Zurück zur Natur

Ich bin fertig.

Jetzt noch eine Liste der Randbedingungen, die in meiner Analyse stillschweigend vorausgesetzt wurden. Ein ehrlicher Makler hätte alles an den Anfang gestellt. Ich wollte den geneigten Leser damit aber nicht abschrecken:

· Bei mir unterliegen Zinserträge keinem Zufallsfaktor, für alle Erträge wird der Durchschnitt genommen.

· Das Handicap des aktuellen Startspielers, ein wichtiges Regulativ gegen einen frühen Start-Ziel-Sieg, wurde nicht berücksichtigt

· Alle Artefakte werden zum Nominalwert gekauft, es findet keine Versteigerung, kein Preiskampf darum statt.

· Das Kartenlimit und die Karten-Stückelung wurde ziemlich tolerant gehandhabt. In der Simulation wurde allein mit "Augenmaß" darauf geachtet, dass nicht zuviel Geld pro Runde übrig bleibt.

· Das Kapital immer voll einsetzbar. Alle gewünschten Artefakte sind immer in ausreichender Menge vorhanden. (Allerdings habe ich mich freiwillig bei Runensteinen und Charismatikmasken auf zwei Stück pro Spieler beschränkt.)

· Kalamitäten durch Artefakte (wie z.B. Zwangsverkäufe von Edelsteinen durch die Unbeteiligten) wurde durch einen entsprechenden geldwerten Vorteil (geschätzt) des jeweiligen handelnden Spielers ersetzt.

Jetzt darf ein erfahrener Zavandor-Ritter einwenden, diese Randbedingungen seien unzulässig, das Zepter spiele sich doch in Wirklichkeit ganz anders ab. Beispiele:

· Die Zufallschwankungen bei den Zinserträgen können eine knappe Kalkulation leicht mal aus den Angeln heben. Eine winzige Ertragsminderung macht manchmal das Erklimmen einer wichtigen Fortschrittsstufe zunichte.

· Die Artefakte stehen nicht immer zur Verfügung. Durch gezielten Preiskampf kann man einem Mitspieler die Butter vom Brot nehmen.

Diese Einwände sind vollkommen berechtigt.

Aber: Wenn wir uns das alles auch noch vor Augen halten müssen …, ja dann stehen wir alle wieder im Wald.