Autor Alessandro Zucchini Verlag daVinci Editrice S.r.l. erschienen 2005 Spielerzahl 2-5 Spielzeit 15 Minuten

Palatinus

rezensiert von Walter Sorger

Mit regelmäßigen Sechsecken läßt sich bekanntlich jede beliebige Fläche babyleicht füllen. (Nur die Ränder brauchen ein bißchen Integralrechung.) In einer solchen Fläche besitzt jedes Teilchen um sich herum genau 6 Nachbarn. Die jeweils 6 Nachbarn zusammen mit dem Zentralstück bilden wieder eine symmetrisches Flächenstück ("Hügel"), mit dem jede beliebige Gesamtfläche gefüllt werden kann.

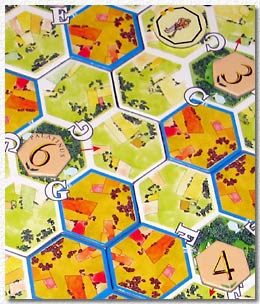
Im Spiel "Palatinus" bilden 7 solcher "Hügel" die Stadtfläche von Rom. Die Sechsecke des Hügels sind in Wälder, Wiesen und Weiden aufgeteilt, die jeweils unterschiedliche Wohnqualität, sprich Siegpunkte für ihren Besitzer bedeuten. Jeder Spieler bekommt sieben Chips, die er im Laufe des Spiels auf den insgesamt 49 Sechsecken verteilt. Reihum legt jeder Spieler einen Chip, und wenn alle Chips gelegt sind, ist das Spiel zu Ende und der Sieger wird ausgerechnet. Wer mit der Summe seiner Chips die lukrativsten Gebiete besetzen konnte hat gewonnen.

Die einzelnen Chips stellen verschiedene Berufsgruppen dar (Händler, Bauern und Heerführer) und liefern unterschiedlich viele Punkte zum Gesamtertrag:

• Der Heerführer zählt auf seinen 6 Nachbarfeldern die Händlern und Bauern. Gibt es hier von einer Berufsgruppe eine Mehrheit, so werden alle entsprechenden Chips entfernt und der Heerführer bekommt für jeden Chip einen Siegpunkt.
  
  
• Mit ihren übrig gebliebenen Händlern und Bauern wetteifern die Spieler um die Kontrolle der einzelnen Hügel.
  
  
• Jeder Bauer bekommt Einflußpunkte für leere Felder und Weideland in seiner Nachbarschaft.
  
  
• Jeder Händler bekommt Einflußpunkte für die verbliebenen Konsumenten in seiner Umgebung.
  
  
• Der Spieler mit den meisten Einflußpunkten auf einem Hügel bekommt dafür ein definierte Anzahl Siegpunkte, alle anderen gehen leer aus.

Das optimale Legen der Chips auf die Stadtfläche entspricht dem Lösen eines Gleichungssystems mit 49 Bekannten (=Sechsecke in Rom) und 35 Unbekannten (=Chips in den Händen der Spieler). Da können die menschlichen Gehirnleitungen ganz schön zum Glühen gebracht werden.

Doch um den rechnerischen Charakter dieser Aufgabe ein bißchen ins Spielerische zu verschieben, werden 3 Chips eines jeden Spielers verkleidet ins Rennen geschickt: Bauern oder Händler treten im Wolfspelz auf und müssen erst am Spielende bei der Siegpunkt-Auswertung ihre Identität offenbaren.

Dadurch kommen ins Gleichungssystem noch zusätzlich 12 stochastische Mengenfunktionen hinzu. Allein vom Fachgebiet her ergibt sich daraus schon eine ganz andere Aufgabenstellung. Erst waren wir bei Punkt- und Strichrechung, jetzt sind wir bei Wahrscheinlichkeitsrechung und Statistik. Auch der stärkste Spiel-Computer der Welt würde für jeden Zug schon einige Tage brauchen, um die Flächen bester Siegpunkt-Erträge berechnen und ausweisen zu können. (Heiliger Bill Gates, steh mir bei!)

Als Folge dieser Verhältnisse hängt man seine Rechen-Ambitionen am besten an den Nagel und betrachtet "Palatinus" als ein hübsches Legespiel, ein konstruktives Anreichern einer gefälligen Landschaft mit Personen, denen wir nahestehen. Das kann immer noch Spaß machen: Kein Kampf, keine Aggressionen, keine Verdrängung, nur Aufbau und Erfüllung. Es geht sehr vor allem flott über die Bühne. Wenn 5 Spieler für jeden einzelnen Zug durchschnittlich 8 Sekunden brauchen, ist das Spiel nach 4,66 Minuten zu Ende.

Die Siegpunkt-Auswertung am Schluß nehmen wir als verdiente oder unverdiente Weihnachtsbescherung mit in Kauf. Der Rechenvorgang dauert in jedem Fall allerdings deutlich länger als die entsprechenden Offenbarungen am Heiligen Abend. Da müssen noch mal 35 Chips mit ihren insgesamt 210 Nachbar-Sechsecken betrachtet, gezählt und verglichen werden. Selbst bei Zuhilfenahme der mitgelieferten individualisierten Kramerleiste wird da noch mal der heiße Schweiß von der Stirne tropfen. Vielleicht sollten wir hier endlich unseren Spiel-Computer zum Einsatz bringen. Spätestens dann, wenn unser fleißiger Günther dazu ein Programm geschrieben hat.

Kommentare lesen/eingeben

©2005, Westpark Gamers