| Autor | Donald X. Vaccarino |
| Verlag | Hans im Glück Verlag |
| erschienen | 2008 |
| Spielerzahl | 2-4 |
| Spieldauer | 45 Minuten |
| Wertung |           |
|
|
||||||||||||
|
von Günther Rosenbaum
Mittlerweile begeistert Dominion schon viele Spieler (mich auch) - und wie immer in so einem Fall, gibt es auch schon viele Analysen, Strategien, Vorschläge für Killerstrategien und unbewiesene Behauptungen über gute und schlechte Strategien im Internet.
Dies hat mich dazu angeregt, mittels "Monte Carlo Methoden" einige objektive Zahlen zur Diskussion beizusteuern (solche Ansätze gibt es hier und da auch schon an anderer Stelle im Internet, z.B. auf http://www.boardgamegeek.com/boardgame/36218 oder http://das-spielen.de/index.php/category/spiele/strategie-und-taktik/): Mittels eines kleinen Java-Simulationsprogrammes werden einige Strategien 1.000.000 mal auf dem PC simuliert und statistische Aussagen hieraus abgeleitet!
Über die Menge der Interaktionsmöglichkeiten in Dominion wurde schon viel gestritten und einige Spieler finden diese sogar zu gering. An dieser Stelle soll daher auf Interaktionen gänzlich verzichtet werden (d.h. ohne Angriffskarten) und stattdessen versucht werden, möglichst schnell eine vorgegebene Anzahl Provinzen (=6 Punkte) zu kaufen! Dieses kann dann zur Bewertung der Strategien in einem Mehrpersonenspiel dienen, denn auch hier ist es ganz wichtig, das Timing zu beachten: Es gilt bei Spielende, z.B. Verkauf aller Provinzen, die meisten Siegpunkte zu besitzen - das Potential eines "Killerdecks" in späteren Phasen ist dann unerheblich.
Außerdem ist die Anzahl der zusätzlichen Siegpunkte beschränkt (Ausnahme "Gärten"): 12*(6+3+1) = 120. Sich frühzeitig einen gehörigen Anteil dieser Punkte zu sichern ist also ein wesentlicher Teil einer jeden guten Strategie!
Betrachten wir zuerst also folgende, häufig im Internet als "Killerstrategie" bezeichnete "Nur-Geld-Strategie":
| Nur-Geld-Strategie |
|
Diese Strategie ohne jegliche Aktionskarten ist sehr einfach und doch schon ziemlich stark! Jede andere Strategie wird sich mit dieser Strategie messen müssen!
Meine Simulation ergibt folgende Ergebnisse:
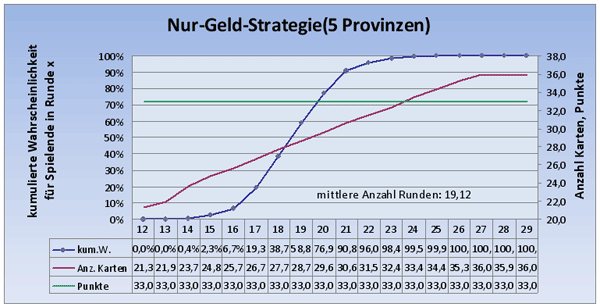
Das Ergebnis ist folgendermaßen zu interpretieren:
Auf der x-Achse ist die Anzahl Runden aufgeführt, in der die Endebedingung (5 Provinzen) erreicht wurde. Betrachten wir die Runde 20: 76,9% aller Spiele dauerten höchstens 20 Runden; die Endpunktzahl dieser Spiele betrug im Mittel 33,00 Punkte; der Spieler besaß am Spielende im Mittel 29,6 Karten!
Die mittlere Rundenanzahl aller Spiele beträgt 19,12!
Die Anzahl der benötigten Runden, um 5 Provinzen zu erreichen, schwankt zwischen 12 und 29; die meisten Spiele enden aber zwischen 17 und 21 Runden. Da man in einem Mehrpersonenspiel selten mehr als 5 Provinzen besitzen wird, so sollte man bei einem Spiel mit wenig Interaktion wohl nicht von mehr als 20 Runden bis Spielende ausgehen.
Betrachten wir nun die Änderung der Berechnung, wenn wir das Spiel schon nach dem Kauf der 4. Provinz beenden:
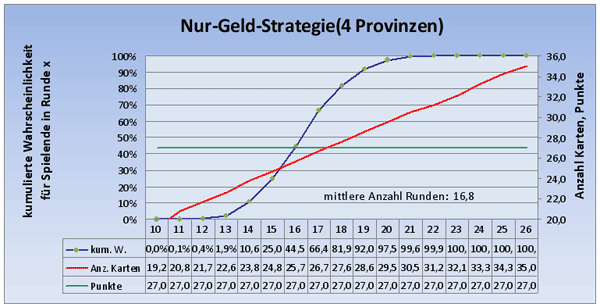
Die mittlere Rundenanzahl bis Spielende fällt jetzt auf 16,8 (bei 6 Provinzen steigt sie auf 21,43).
Bei dieser Strategie wird man also gegen Spielende in etwa nur jede zweite Runde in der Lage sein eine Provinz zu kaufen! Die Anzahl der Karten steigt trotzdem pro Runde um etwa 1, da man alternativ ja ein Silber oder Gold kauft.
Bleiben wir aber momentan weiterhin bei beim Spielende mit 5 Provinzen und modifizieren wir unsere Geldstrategie etwas: Sobald wir zum ersten mal in der Lage sind eine Provinz zu kaufen, so verweigern wir dies und kaufen stattdessen doch nur ein Gold! In einigen Strategieanalysen wird behauptet, dass dies die Strategie verbessert:
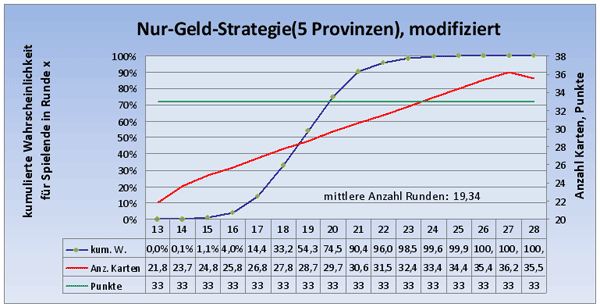
Dies kann ich hier nicht nachvollziehen - die mittlere Rundenanzahl wird geringfügig schlechter. Also. Wenn man 8 Geld auf der Hand hält, so sollte man dafür auch eine Provinz kaufen!
Nehmen wir nun noch eine Schmiede mit in das Deck, um mehr Karten auf die Hand zu bekommen, die "Geld-Schmiede-Strategie":
| Geld-Schmiede-Strategie |
|
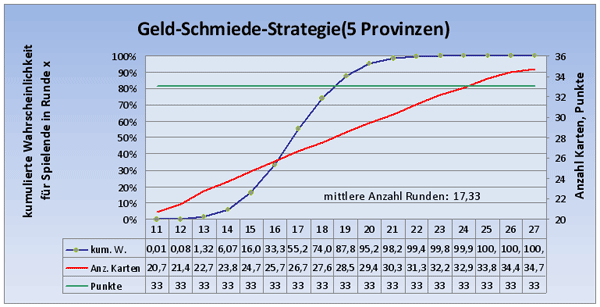
Die mittlere Rundeanzahl ist hier schon deutlich verbessert worden (bei 4 Provinzen: 14,93, bei 6: 19,69). Allerdings ist hier auch nur genau eine Schmiede hilfreich: Nehme ich eine zweite hinzu, so bleibt das Deck in etwa gleich gut, nehme ich eine dritte hinzu, so wird es sichtbar schlechter.
Die nächste Strategie, die ich betrachten möchte, ist die "Geld-Kapelle-Strategie":
| Geld-Kapelle-Strategie |
|
Hier versuchen wir, unsere Handkarten von störenden Karten freizuhalten und sie möglichst früh zu entsorgen:
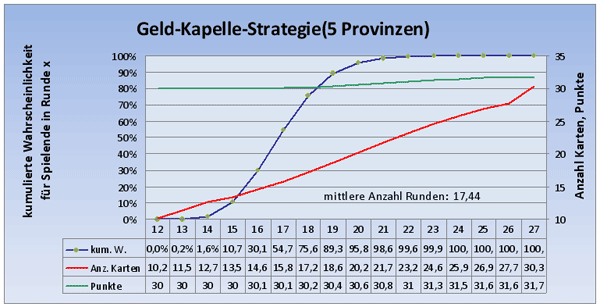
Die mittlere Rundenanzahl ist um knapp 2 Runden gefallen auf 17,44 ; die meisten Partien laufen 15 bis 19 Runden. Mit dieser Strategie sind wir also im Allgemeinen etwas schneller und damit besser als die Nur-Geld-Strategie! In den schnellen Partien hat man die Kupfer und Anwesen schnell entsorgen können und bei 17 Runden hat man am Ende nur ca. 16 Karten im eigenen Deck.
Beendet man das Spiel bei 4 bzw. 6 Provinzen, so dauert das Spiel im Mittel 15,43 bzw. 19,5 Runden. Also auch hier braucht man für eine Provinz mehr oder weniger jeweils 2 Runden. Als Daumenregel erhält man also in etwa: Anzahl Runden = 7,5 + 2 * Anzahl Provinzen.
Wir wollen das Spiel jetzt noch mehr beschleunigen und nehmen noch einige Laboratorien(+2 Karten, + 1 Aktion) mit in unser Kartendeck. Die optimale Anzahl wurde durch Simulationen bestimmt, die "Geld-Kapelle-Labor-Strategie":
| Geld-Kapelle-Labor-Strategie |
|
Hier versuchen wir, unser Deck ähnlich klein zu halten und durch die "+2 Karten" Aktion des Labors noch mehr Karten auf die Hand zu bekommen; außerdem können wir durch das Labor weitere Aktionen ausführen.
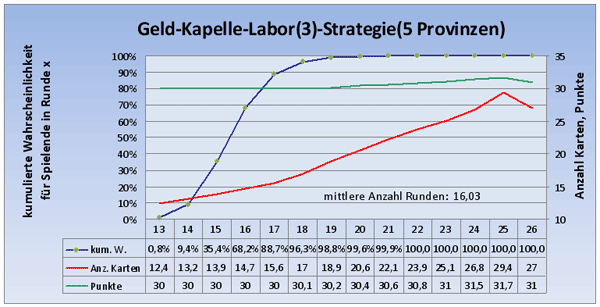
Die mittlere Anzahl Runden ist hier nochmal gefallen auf 16,03!
Zu- oder wegnehmen eines Labors führt zu einer Verschlechterung der Rundenanzahl - somit sind hier 3 Laboratorien optimal. Auch das Entsorgen von Silber bei genügendem Gold hilft nicht mehr und führt zu gleichen Ergebnissen.
Zum Schluss betrachte ich jetzt noch eine Strategie mit massiverem Aktionskarteneinsatz und "virtuellem" Geld, die "Jahrmarkt-Schmiede-Strategie":
| Geld- Jahrmarkt(1)-Schmiede(2)-Strategie |
|
Wir wollen hier zuerst mit einem Jahrmarkt und 2 Schmieden spielen. Jahrmarkt und Schmieden sollen Kettenreaktionen hervorrufen (wenn noch mehr Aktionskarten genommen werden) und zusätzlich soll virtuelles Geld ins Spiel kommen.
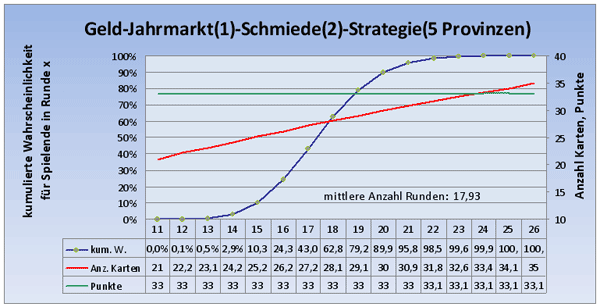
Die Kurve ist flacher und die Anzahl der Runden variiert etwas mehr als im vorherigen Bild.
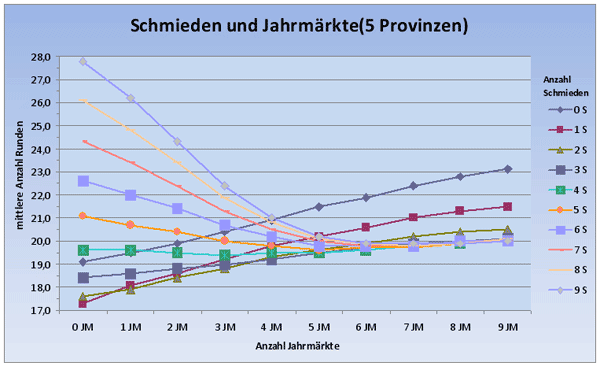
Wir wollen aber nun schauen was passiert, wenn wir die Anzahl der Jahrmärkte und Schmieden jeweils im Bereich von 0 bis 9 variieren und berechnen für jede Kombination die mittlere Anzahl Runden bis zum Erreichen von 5 Provinzen:
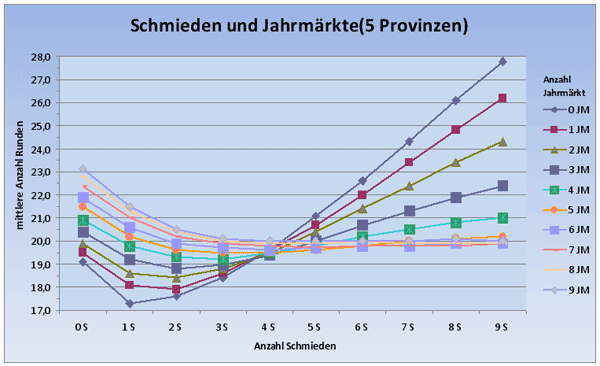
In der obigen Grafik sehen wir, wie sich für eine feste Anzahl von Jahrmärkten (die lila Kurve beschreibt z.B. 3 Jahrmärkte) die mittlere Anzahl von Runden verändert, wenn wir zwischen 0 und 9 Schmieden ins Deck mit hinzugeben. Das absolute Minimum dieser Kurvenschar wird bei einer Schmiede und keinem Jahrmarkt erreicht - auch hier sieht man wieder, dass die sehr schnellen Decks mit wenig Aktionskarten auskommen.
Aber auch 4 Schmieden und 5 Jahrmärkte sind in etwas gleich schnell wie das Nur-Geld-Deck! Man kann also auch mit massivem Aktionskarteneinsatz ähnlich schnelle Decks wie mit der Nur-Geld-Strategie aufbauen.
Mit den gleichen Daten - aber mit fester Anzahl von Schmieden und variabler Anzahl von Jahrmärkten - erhält man folgendes Diagramm:
Zur Veranschaulichung betrachten wir hier den exemplarisches Ablauf eines 19-Runden Spieles mit 4 Schmieden und 5 Jahrmärkten:
("Kauf: nix" bedeutet: es ist eine Kaufaktion verfügbar, es wird aber nichts gekauft)
Betrachten wir nun noch einmal alle oben diskutierten Strategien im Überblick:
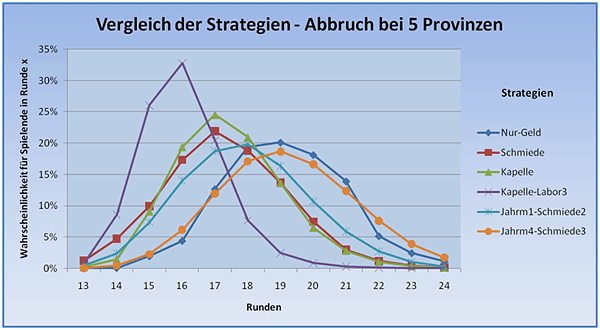
Es tritt hier besonders die Strategie mit "einer Kapelle und 3 Laboratorien" hervor - sie ist sehr schnell und variiert in der Anzahl der Runden nicht so stark. Die Unterschiede der anderen Strategien sind zwar gut erkennbar, jedoch überschneiden sie sich sehr stark.
Genügen diese Unterschiede, um z.B. in einem Zweipersonenspiel signifikante Vorteile der Kapellenstrategie gegenüber der Nur-Geld Strategie zu erkennen? Diese Frage werden wir im zweiten Teil der Analyse beantworten; dort werden wir Mehrpersonenspiele betrachten, die beendet werden, wenn der Stapel der Provinzen leergekauft wurde.
| Kommentare lesen/schreiben |
©2009, Westpark Gamers